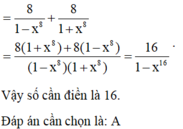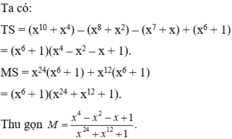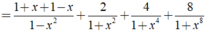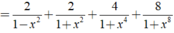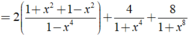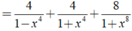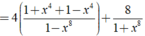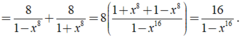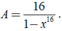Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\\ =\left(x^{64}-1\right)-x^{64}\\ =-1\)
Vậy đa thức ko phụ thuộc vào x
\(C=(x^2-1)(x^2+1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^4-1)(x^4+1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^8-1)(x^8+1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{16}-1)(x^{16}+1)(x^{32}+1)-x^{64}\\=(x^{32}-1)(x^{32}+1)-x^{64}\\=x^{64}-1-x^{64}\\=-1\)
⇒ Giá trị của C không phụ thuộc vào giá trị của biến

a: \(x^4+4=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-x^6-x^5-x^4+x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
c: \(x^8+x^4+1\)
\(=\left(x^8+2x^4+1\right)-x^4\)
\(=\left(x^4-x^2+1\right)\cdot\left(x^4+x^2+1\right)\)
\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)

Áp dụng (a-b) (a + b) = a 2 - b 2 . Ta có:
M = 1 1 − x 2 . 1 1 + x 2 . 1 1 + x 4 . 1 1 + x 8 . 1 1 + x 16
= 1 1 − x 16 . 1 1 + x 16 = 1 1 − x 32

1) \(x^2-7x+6=x^3+1-7x-7=\left(x^3+1\right)-7\left(x+1\right)=\left(x+1\right)\left(x^2-x-6\right)\)
2) \(x^3-9x^2+6x+16\)
\(\left(x^3+1\right)-\left[\left(9x^2-6x+1\right)-16\right]\)
\(=\left(x^3+1\right)-\left[\left(3x-1\right)^2-16\right]=\left(x^3+1\right)-\left(3x-1+4\right)\left(3x-1-4\right)\)\(=\left(x^3+1\right)-3\left(3x-5\right)\left(x+1\right)\)\(=\left(x+1\right)\left[x^2-x+1-9x+15\right]=\left(x+1\right)\left(x^2-10x+16\right)\)
\(=\left(x+1\right)\left[x\left(x-2\right)-8\left(x-2\right)\right]\)\(\left(x+1\right)\left(x-2\right)\left(x-8\right)\)
3) \(x^3-6x^2-x+30\)
\(=x^3-5x^2-x^2+5x-6x+30\)
\(=x^2\left(x-5\right)-x\left(x-5\right)-6\left(x-5\right)\)
\(=\left(x-5\right)\left(x^2-x-1\right)\)
4) \(2x^3-x^2+5x+3=\left(2x^3+x^2\right)-\left(2x^2+x\right)+\left(6x+3\right)\)
\(=x^2\left(2x+1\right)-x\left(2x+1\right)+3\left(2x+1\right)\)
\(=\left(2x+1\right)\left(x^2-x+3\right)\)
5) \(27x^3-27x^2+18x-4=\left(27x^3-1\right)-\left(27x^2-18x+3\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(9x^2-6x+1\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(3x-1\right)^2\)
\(=\left(3x-1\right)\left(9x^2+3x+1-9x+3\right)=\left(3x-1\right)\left(9x^2-6x+4\right)\)
gửi phần này trước còn lại làm sau !!! tk mk nka !!!

2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)