Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có : tổng ba góc của 1 tam giác bằng 180 độ => góc A = 180 -( b+c) = 180 - 100 = 80
vì tia AD là tia phân giác của góc A nên : góc ADC = góc ADB = 1/2 góc A = 1/2. 80 =40

Ta có:
\(b^2=ac\rightarrow\frac{a}{b}=\frac{b}{c}\) ( \(b\ne0,c\ne0\)
\(c^2=bd\rightarrow\frac{b}{c}=\frac{c}{d}\) \(d\ne0\)
\(\Rightarrow\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\rightarrow\frac{abc}{bcd}=\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}\) ( \(bcd\ne0\)vì \(b^3+c^3+d^3\ne0\))
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}\rightarrow\frac{abc}{bcd}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
\(\frac{abc}{bcd}=\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}=\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\)
\(\Rightarrow\frac{a^3+b^3+c^3}{b^3+c^3+d^3}=\left(\frac{a+b+c}{b+c+d}\right)^3\left(đpcm\right)\)

Bài 2:
Đặt số đo góc B là x, số đo góc C là y
Theo đề, ta có:
\(\left\{{}\begin{matrix}x+y=90\\x-y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=114\\x+y=90\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=57^0\\y=33^0\end{matrix}\right.\)

b) a2=ac\(\Rightarrow\) \(\frac{a}{b}=\frac{b}{c}\)
c2=bd\(\Rightarrow\) \(\frac{b}{c}=\frac{c}{d}\)
\(\Rightarrow\)\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\) = \(\frac{a^3}{b^3}=\frac{b^3}{c^3}=\frac{c^3}{d^3}\) = \(\frac{a^3+b^3+c^3}{b^3+c^3+d^3}\)
=\(\frac{a.b.c}{b.c.d}=\frac{a}{d}\)
=> đpcm

Bài 2:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{b-a}{5-4}=10\)
Do đó:a=40; b=50
b: \(\left\{{}\begin{matrix}\dfrac{a}{b}=\dfrac{2}{3}\\\dfrac{b}{c}=\dfrac{6}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{b}{3}\\\dfrac{b}{6}=\dfrac{c}{5}\end{matrix}\right.\Leftrightarrow\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{5}\)
Đặt \(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{5}=k\)
=>a=4k; b=6k; c=5k
Ta có: \(c^2-a^2=81\)
\(\Leftrightarrow25k^2-16k^2=81\)
\(\Leftrightarrow9k^2=81\)
\(\Leftrightarrow k^2=9\)
Trường hợp 1: k=3
=>a=12; b=18; c=15
Trường hợp 2: k=-3
=>a=-12; b=-18; c=-15

A B C I
Ta có : \(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\frac{\widehat{B}+\widehat{C}}{2}=180^O-\frac{180^O-\widehat{A}}{2}\)
\(=180^O-\frac{180^O-40}{2}=110^O\)
Vậy chọn đáp án C
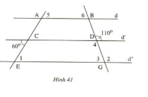
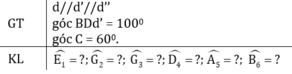

Vì E1 = C = 70 độ ( Vì đó là hai góc so le trong bằng nhau )
Vì G2 = D = 120 độ ( Vì đó là hai góc trong đồng vị bằng nhau )
Vì G2 + G3 = 180 độ ( Vì đó là hai góc kề bù )
T/số : 120 độ + G3 = 180 độ
G3 = 180 độ - 120 độ
G3 = 60 độ
MÌNH GIẢI TRƯỚC CHO BẠN CÁC GÓC NÀY BẠN CÓ THỂ VẼ LẠI HÌNH CHO ĐÚNG HƠN ĐC KO MÌNH THẤY BẠN VẼ HÌNH CÓ CHỖ SAI NHÉ !