
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1:
\(\left(6-\frac{2}{3}+\frac{1}{2}\right)-\left(5+\frac{5}{3}-\frac{3}{2}\right)-\left(3-\frac{7}{3}+\frac{5}{2}\right)\)
\(=\left(\frac{36-4+3}{6}\right)-\left(\frac{30+10-9}{6}\right)-\left(\frac{18-14+15}{6}\right)\)
\(=\frac{35}{6}-\frac{31}{6}-\frac{19}{6}\)
\(=\frac{35-31-19}{6}\)
\(=\frac{-15}{6}=\frac{-5}{2}\)
Cách 2:
\(\left(6-\frac{2}{3}+\frac{1}{2}\right)-\left(5+\frac{5}{3}-\frac{3}{2}\right)-\left(3-\frac{7}{3}+\frac{5}{2}\right)\)
\(=6-\frac{2}{3}+\frac{1}{2}-5-\frac{5}{3}+\frac{3}{2}-3+\frac{7}{3}-\frac{5}{2}\)
\(=6-5-3+\frac{1}{2}+\frac{3}{2}-\frac{5}{2}-\frac{2}{3}-\frac{5}{3}+\frac{7}{3}\)
\(=-2-\frac{1}{2}+0\)
\(=\frac{-5}{2}\)
= \(6-\frac{2}{3}+\frac{1}{2}-5-\frac{5}{3}+\frac{3}{2}-3+\frac{7}{3}-\frac{5}{2}\)
\(=\left(-\frac{2}{3}-\frac{5}{3}+\frac{7}{3}\right)+\left(\frac{1}{2}+\frac{3}{2}-\frac{5}{2}\right)+\left(6-5-3\right)=0-\frac{1}{2}-2=-\frac{5}{2}\)

c1:Thay số
Q=\(\frac{5+2.4-3.3}{5-2.4+3.3}\)
O=\(\frac{4}{6}\)=\(\frac{2}{3}\)
\(\frac{4x}{6y}=\frac{2x+8}{3y+11}\)
\(4x\left(3y+1\right)=6y\left(2x+8\right)\)
\(12xy+4x=12xy+48y\)
\(4x-48y=0\)
\(4x=48y\)
Ta có:\(\frac{4x}{48y}\)
\(\Leftrightarrow\)\(\frac{x}{y}=\frac{1}{12}\)

c1: EF=5cm
c2: EF=\(5\sqrt{2}\)cm
c3: \(DF=\sqrt{119}cm\)
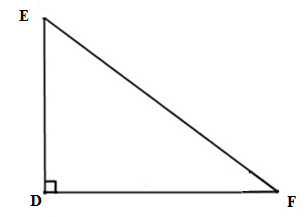
a) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=3^2+4^2\)
=> \(EF^2=9+16\)
=> \(EF^2=25\)
=> \(EF=5\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\left(cm\right).\)
b) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=5^2+5^2\)
=> \(EF^2=25+25\)
=> \(EF^2=50\)
=> \(EF=\sqrt{50}\)
=> \(EF=5\sqrt{2}\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\sqrt{2}\left(cm\right).\)
c) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(12^2=5^2+DF^2\)
=> \(DF^2=12^2-5^2\)
=> \(DF^2=144-25\)
=> \(DF^2=119\)
=> \(DF=\sqrt{119}\left(cm\right)\) (vì \(DF>0\)).
Vậy \(DF=\sqrt{119}\left(cm\right).\)
Chúc bạn học tốt!

\(A=6-\dfrac{2}{3}+\dfrac{1}{2}-5-\dfrac{5}{3}+\dfrac{3}{2}-3-\dfrac{5}{2}+\dfrac{7}{3}\)
\(=-2-\dfrac{1}{2}=-\dfrac{5}{2}\)

C1:sử dụng chương trình bảng tính khi:
-Thực hiện các phép tính từ đơn giản đến phức tạp
-Liệt kê các đối tượng dưới dạng bảng
-Tạo các biểu đồ biểu diễn trực quan các số liệu trong bảng
............................................
C2: địa chỉ khối là:cặp địa chỉ của ô trên cùng bên trái và ô dưới cùng bên phải ,được phân cách bởi dấu":"

\(\hept{\begin{cases}\frac{a}{a1}=\frac{b}{b1}=\frac{c}{c1}=3\\\frac{2a-3b}{2a1-3b1}=3\end{cases}\Rightarrow3=\frac{2a-3b}{2a1-3b1}=\frac{c}{c1}=\frac{2a-3b+c}{2a1-3b1+c1}}\).Vậy\(\frac{2a-3b+c}{2a1-3b1+c1}=3\)