Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách lớn nhất từ giả thiết nghĩa là khoảng cách từ vân sáng bậc 2 (nửa trên) đến vân tối thứ 4 (nửa dưới)
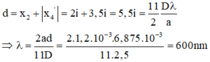
Đáp án D

Chọn C
Ta có: i = λD/a = 2mm.
Số vân sáng trên màn là:
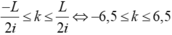
=> Có 13 giá trị của k thỏa mãn
Vậy trên màn có 13 vân sáng

Đáp án D
Khoảng vân là:
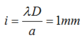
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là :
![]()

Phương pháp: áp dụng công thức tính khoảng vân và công thức xác định vị trí vân sáng
Cách giải: Khoảng vân là: i = λ D a = 1 m m
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là
![]()
Đáp án D

Khoảng vân giao thoa :
![]()
Số khoảng vân trong một nửa bề rộng của miền giao thoa :
![]()
Số vân sáng trong một nửa bề rộng, không kể vân trung tâm là 4 vân. Số vân sáng trong cả bề rộng của miền giao thoa, kể cả vân trung tâm :
(2.4) + 1 = 9 vân
Số vân tối trong một nửa bề rộng : 4 vân.
Số vân tối trong cả bề rộng của miền giao thoa : 2. 4 = 8 vân.
Tổng số vân sáng và vân tối trong miền giao thoa : 9 + 8 = 17 vân.

\(i = \frac{\lambda D}{a}= \frac{0,6.2,5}{1}=1,5 mm.\)
Số vân sáng quan sát trên màn
\(N_s = 2.[\frac{L}{2i}]+1=2.4+1 = 9.\)
Số vân tối quan sát trên màn
\(N_t = 2[\frac{L}{2i}+0,5]=2.4 = 8.\)
Tổng số vân sáng và vân tối là
\(N = N_t + N_s = 9+8 = 17.\)