Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Phương pháp:
Chia khối lập phương, nhận xét các khối tạo thành và tính thể tích của chúng
Cách giải:
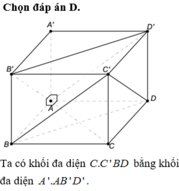
Chia khối lập phương ABC.A’B’C’ bởi mặt phẳng (AB’D’) và (C’BD) ta được:
+) Chóp A.A’B’D’
+) Chóp C’.BCD
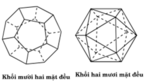
+) Khối bát diện ABD.B’C’D’
Ta có
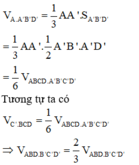
Các khối A.A’B’D’ và C’.BCD không phải là chóp tam giác đều và khối bắt diện ABD.B’C’D’ không phải là khói bát diện đều
Do đó chỉ có mệnh đề III đúng

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15

Chia khối lập phương ABCD.A'B'C'D' thành năm khối tứ diện như sau:AB'CD', A'AB'D', BACB', C'B'CD', DACD'.

Chia khối lập phương ABCD.A'B'C'D' thành năm khối tứ diện như sau:A'B'CD', A'AB'D', BACB', C'B'CD', DACD'.
Chia khối lập phương ABCD.A’B’C’D’ thành năm khối tứ diện như sau: AB’CD’, A’AB’D’, BACB’, C’B’CD’, DACD’.


Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.

Một số khi chia cho 4 có 4 khả năng: chia hết (có dạng 4k), dư 1 (có dạng 4k + 1), dư 2 (có dạng 4k + 2), dư 3 (có dạng 4k + 3 = 4(k+1) - 1 = 4n - 1, với n = k+1).
Vì số nguyên tố lớn hơn 2 nên số đó không chia hết cho 2 => số đó không chia hết cho 2 và cho 4. Vậy nó chỉ có dạng 4k + 1 hoặc 4n - 1

Đáp án A
Nếu số mặt là 6 dễ thấy số cạnh là 9, nếu số mặt là 4 thì số cạnh là 6 do đó (2) sai.
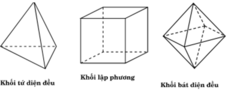
Đáp án C
Chú ý vào tên gọi của nó thể hiện rõ điều này.