Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
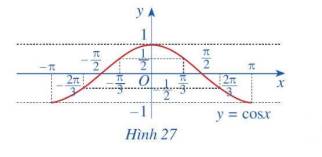
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
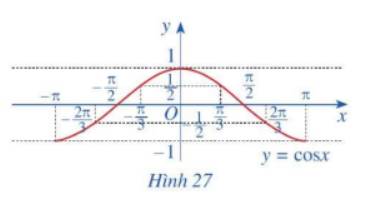
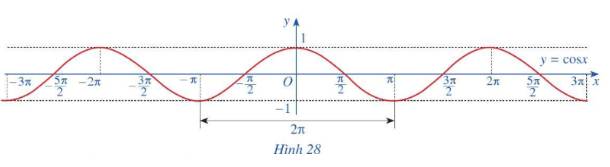
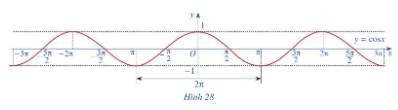
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

a)
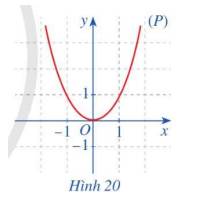
Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
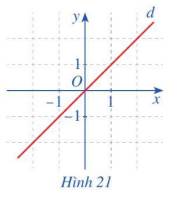
Ta có: \(g\left( { - x} \right) = - g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d

Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.

Ta có: \(s\in\left[-1;1\right]\Leftrightarrow-1\le2cos\left(\pi t\right)\le1\\ \Leftrightarrow-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\)
Trong 1s đầu tiên \(0< t< 1\Rightarrow0< \pi t< \pi\)
Ta có đồ thị hàm số \(y=cos\left(x\right)\) trên \(\left[0;\pi\right]\)
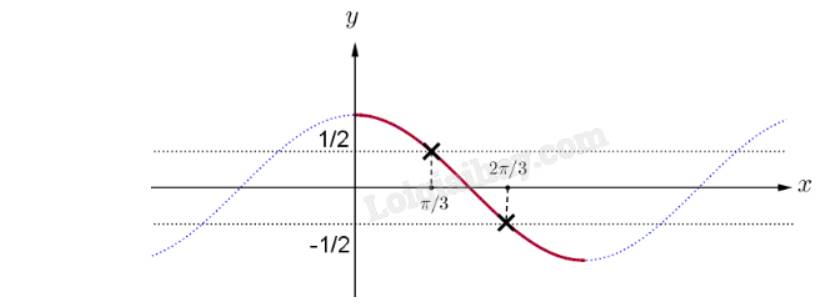
Dựa vào đồ thị, ta thấy
\(-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\Leftrightarrow\dfrac{\pi}{3}\le\pi t\le\dfrac{2\pi}{3}\Leftrightarrow\dfrac{1}{3}\le t\le\dfrac{2}{3}\)
Vậy \(t\in\left[\dfrac{1}{3};\dfrac{2}{3}\right]\)

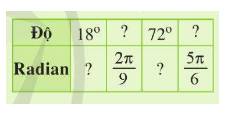
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

Tham khảo:
a,

\(\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2\)
b) Lấy dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta có \(f\left( {{x_n}} \right) = 2{x_n}.\)
\(\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2\)

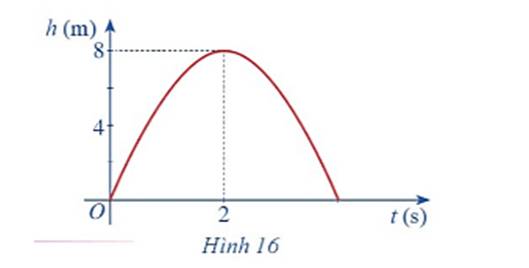
a) Hàm số \(h\left( t \right) = - 2{t^2} + 8t\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) do đó hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hàm số khi t tiến dần đến 2 thì h(t) dần đến 8.
Vậy \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right) = 8\)

a)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).


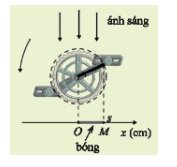






a) Sau t giây điểm M quét được một góc lượng giác có số đo là: \(\alpha = \frac{\pi }{{10}}t\) rad.
Xét tam giác HOM vuông tại O có:
\(MO = tan\alpha .1 = \tan \left( {\frac{\pi }{{10}}t} \right)\).
Vậy tọa độ \({y_M} = \tan \left( {\frac{\pi }{{10}}t} \right)\).
b) Xét \(\tan \left( {\frac{\pi }{{10}}t} \right) = - 1\)
\(\begin{array}{l} \Leftrightarrow \tan \left( {\frac{\pi }{{10}}t} \right) = \tan \left( { - \frac{\pi }{4}} \right)\\ \Leftrightarrow \frac{\pi }{{10}}t = - \frac{\pi }{4} + k\pi \\ \Leftrightarrow t = - \frac{5}{2} + 10k,k \in \mathbb{Z}.\end{array}\)
Vì \(t \ge 0\) nên tại các thời điểm \(t = - \frac{5}{2} + 10k,k \in \mathbb{Z},k \ge 1\) thì đèn hải đăng chiếu vào ngôi nhà.