Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: 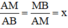
⇒ AM = x.AB = ax;
⇒ M B = x . A M = x . a x = a x 2
Ta có: MA + MB = AB
⇒ a x + a x 2 = a ⇔ x 2 + x = 1 ⇔ x 2 + x − 1 = 0
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
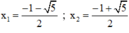
Chỉ có nghiệm 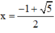 thỏa mãn điều kiện.
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: 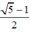
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi M là điểm chia đoạn AB (AM > MB) và AB có độ dài bằng a.
Gọi tỉ số cần tìm là x (x > 0).
Theo đề bài: 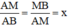
⇒ AM = x.AB = ax;
⇒MB = x.AM = x.ax = ax2
Ta có: MA + MB = AB
⇒ ax + ax2 = a
⇔ x2 + x = 1
⇔ x2 + x – 1 = 0.
Có a = 1 ; b = 1 ; c = -1 ⇒ Δ = 1 – 4.1.(-1) = 5 > 0.
Phương trình có hai nghiệm
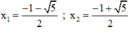
Chỉ có nghiệm 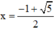 thỏa mãn điều kiện.
thỏa mãn điều kiện.
Vậy tỉ số cần tìm là: 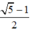

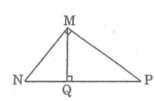
N M Q P
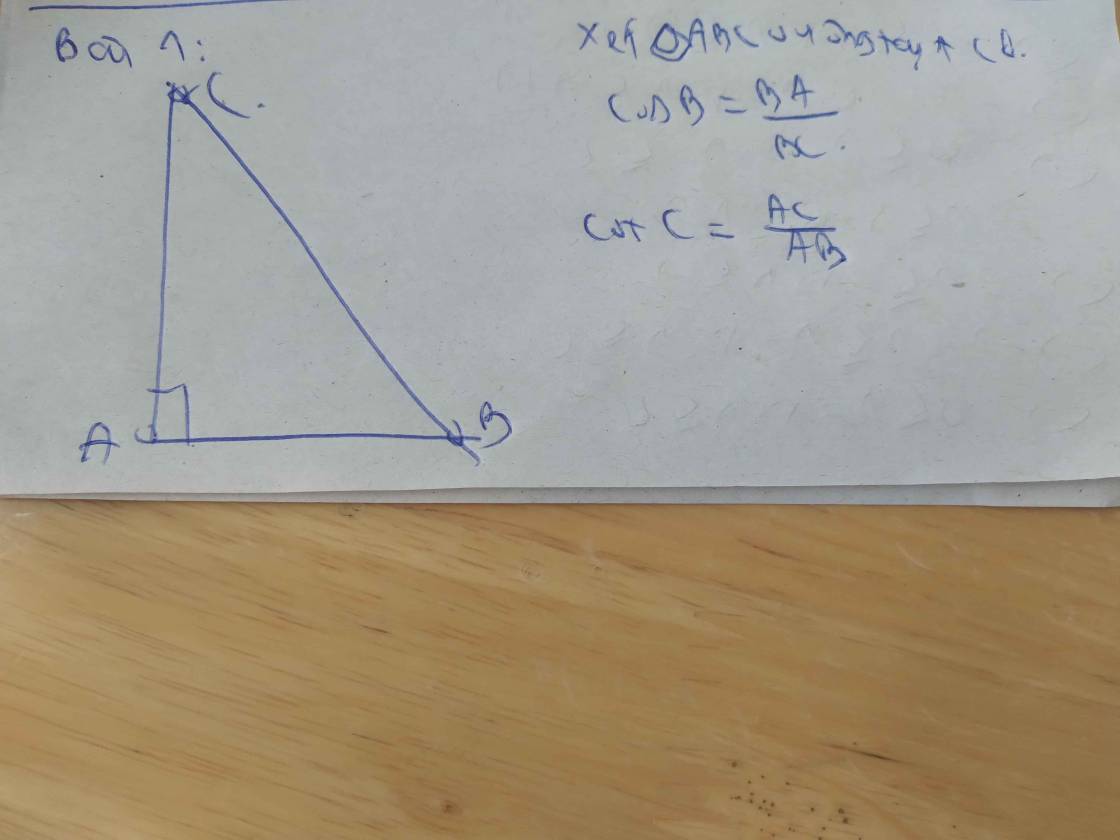
Trong tam giác MNQ vuông tại Q , ta có :
\(cotg \widehat{N}=\frac{NQ}{MQ}=\frac{3}{MQ}\)
Tam giác MPQ vuông tại Q , ta có :
\(cotg \widehat{P} =\frac{PQ}{MQ}=\frac{6}{MQ}\)
Ta có : \(\frac{6}{MQ}>\frac{3}{MQ}\)nên \(cotg \widehat{P } > cotg \widehat{N}\)
\(\frac{cotg \widehat{P}}{cotg \widehat{N}}=\frac{\frac{6}{MQ}}{\frac{3}{MQ}}=\frac{6}{MQ}.\frac{MQ}{3}=\frac{6}{3}=2\)
Vậy : \(cotg \widehat{P} =2cotg \widehat{N}\)

\(MQ=\sqrt{3\cdot6}=3\sqrt{2}\left(cm\right)\)
\(\cot N=\dfrac{NQ}{MQ}=\dfrac{3}{3\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\cot P=\dfrac{MQ}{PQ}=\dfrac{3\sqrt{2}}{6}=\dfrac{\sqrt{2}}{2}\)
Do đó: \(\cot N=\cot P\)




A M B
Giải:
Giả sử \(M\) là điểm chia đoạn \(AB\) và \(AB\) có độ dài bằng \(a\)
Gọi độ dài của \(AM=x;0< x< a\). Khi đó \(MB=a-x\)
Theo đề bài ta có:
\(\dfrac{AM}{AB}=\dfrac{MB}{AM}\) Hay \(\dfrac{x}{a}=\dfrac{a-x}{x}\)
Giải phương trình \(x^2=a\left(a-x\right)\) Hay \(x^2+ax-a^2=0\)
\(\Delta=a^2+4a^2=5a^2;\sqrt{\Delta}=a\sqrt{5}\)
\(x_1=\dfrac{-a+a\sqrt{5}}{2}=\dfrac{a\left(\sqrt{5}-1\right)}{2}\)
\(x_2=\dfrac{-a\left(\sqrt{5}+1\right)}{2}\)
Vì \(x>0\) nên \(x_2\) không thỏa mãn điều kiện của ẩn
Vậy \(AM=\dfrac{a\left(\sqrt{5}-1\right)}{2}\)
Vậy tỉ số cần tìm là \(\dfrac{AM}{AB}=\dfrac{\sqrt{5}-1}{2}\)