Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số vận động viên tham gia là: \(n = 5 + 12 + 32 + 45 + 30 = 124\).
Gọi \({x_1};{x_2};...;{x_{124}}\) lần lượt là thời gian chạy của 124 vận động viên được xếp theo thứ tự không giảm.
Do \({x_1};...;{x_5} \in \begin{array}{*{20}{l}}{\left[ {21;21,5} \right)}\end{array};{x_6};...;{x_{17}} \in \begin{array}{*{20}{l}}{\left[ {21,5;22} \right)}\end{array};{x_{18}};...;{x_{49}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {22;22,5} \right)}\end{array}}\end{array};\)\({x_{50}};...;{x_{94}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\left[ {22,5;23} \right)}\end{array}}\end{array}}\end{array}\) nên trung vị của mẫu số liệu là: \(\frac{1}{2}\left( {{x_{62}} + {x_{63}}} \right) \in \begin{array}{*{20}{l}}{\left[ {22,5;23} \right)}\end{array}\)
Ta có: \(n = 124;{n_m} = 45;C = 5 + 12 + 32 = 49;{u_m} = 22,5;{u_{m + 1}} = 23\)
Trung vị của thời gian chạy của các vận động viên là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 22,5 + \frac{{\frac{{124}}{2} - 49}}{{45}}.\left( {23 - 22,5} \right) \approx 22,64\)
Vậy ban tổ chức nên chọn các vận động viên có thời gian chạy không quá 22,64 giây

Đáp án A
Số cách lấy ra 4 ứng viên bất kỳ từ 16 ứng viên là ![]() cách.
cách.
- Gọi A là biến cố “4 ứng viên lấy được có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi”. Ta xét ba khả năng sau:
- Số cách lấy 1 10 tuổi, 3 11 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 2 11 tuổi, 1 12 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 1 11 tuổi, 2 12 tuổi là: ![]()
Xác suất của biến cố A là 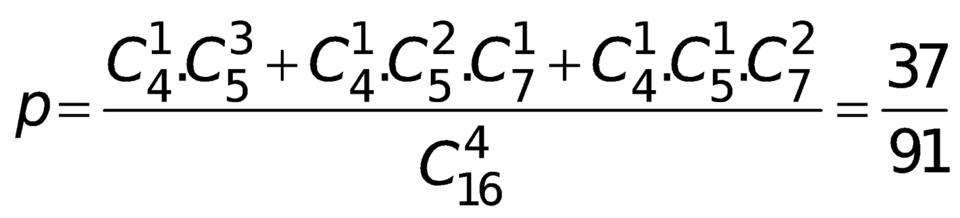 .
.

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5;10)
Ta có \(j = 2,\;{a_2} = 5,\;{m_2} = 16,\;{m_1} = 8;\;{m_3} = 4,\;h = 5.\) Do đó,
\({M_0} = 5 + \frac{{16 - 8}}{{\left( {16 - 8} \right) + \left( {16 - 4} \right)}} \times 5 = 7\).

Chọn C
Gọi biến cố A: “2 giáo viên tập huấn gồm 1 thầy giáo và 1 cô giáo”.
Suy ra ![]() .
.
Vậy 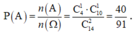 .
.

\(C=M\cup N\)
\(D=M\cap N\)
\(F=M\cap\overline{N}\)
\(G=\left(\overline{N}M\right)\cup\left(\overline{M}N\right)\)

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
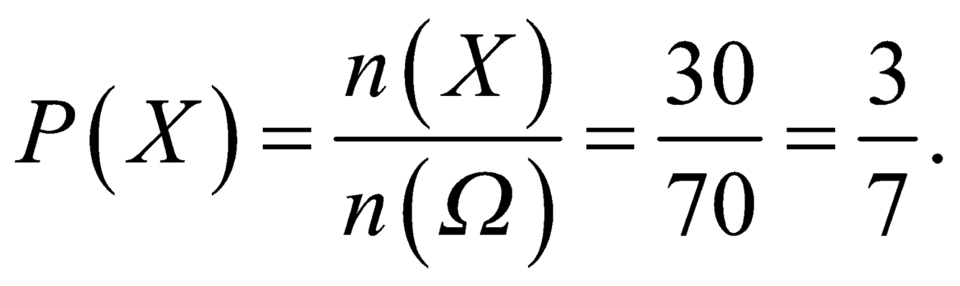


Số vận động viên được khảo sát là \(n = 3 + 8 + 12 + 12 + 4 = 39\).
Gọi \({x_1};{x_2};...;{x_{39}}\) là thời gian luyện tập của 39 vận động viên được xếp theo thứ tự không giảm. Ta phải chọn các vận động viên có thời gian luyện tập tương ứng là \({x_{30}};{x_{31}};...;{x_{39}}\)
Ta có:
\({x_1},{x_2},{x_3} \in \left[ {0;2} \right);{x_4},...,{x_{11}} \in \left[ {2;4} \right);{x_{12}},...,{x_{23}} \in \left[ {4;6} \right);{x_{24}},...,{x_{35}} \in \left[ {6;8} \right);{x_{36}},...,{x_{39}} \in \left[ {8;10} \right)\). Vậy \({x_{30}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array}\).
Ta có: \(n = 29;{n_j} = 12;C = 3 + 8 + 12 = 23;{u_j} = 6;{u_{j + 1}} = 8\)
\({x_{30}} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 6 + \frac{{\frac{{3.39}}{4} - 23}}{{12}}.\left( {8 - 6} \right) \approx 7,04\)
Vậy huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ 7,04 giờ trở lên.