AP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
OM
0
PT
1
CM
14 tháng 1 2017
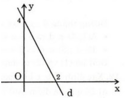
Hàm số y = 4 – 2x có:
+ Tập xác định D = R
+ Có a = –2 < 0 nên hàm số nghịch biến trên R.
+ Tại x = 0 thì y = 4 ⇒ A(0 ; 4) thuộc đồ thị hàm số.
Tại x = 2 thì y = 0 ⇒ B(2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0 ; 4) và B(2; 0).
24 tháng 10 2021
hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)
PT
1
CM
25 tháng 6 2017
Hàm số y = |x + 1|
Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.
Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1.
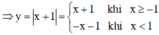
+ Tập xác định: R
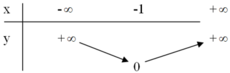
+ Trên (–∞; –1), y = x + 1 đồng biến.
Trên (–1 ; +∞), y = –x – 1 nghịch biến.
Ta có bảng biến thiên :
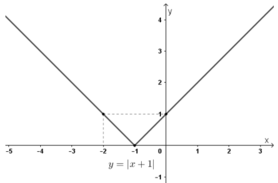
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.
Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.
CN
0
HP
21 tháng 12 2020
a, Bảng biến thiên:
Đồ thị hàm số:
b, Phương trình hoành độ giao điểm
\(-x^2+2x+3=4x-5\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)
Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)