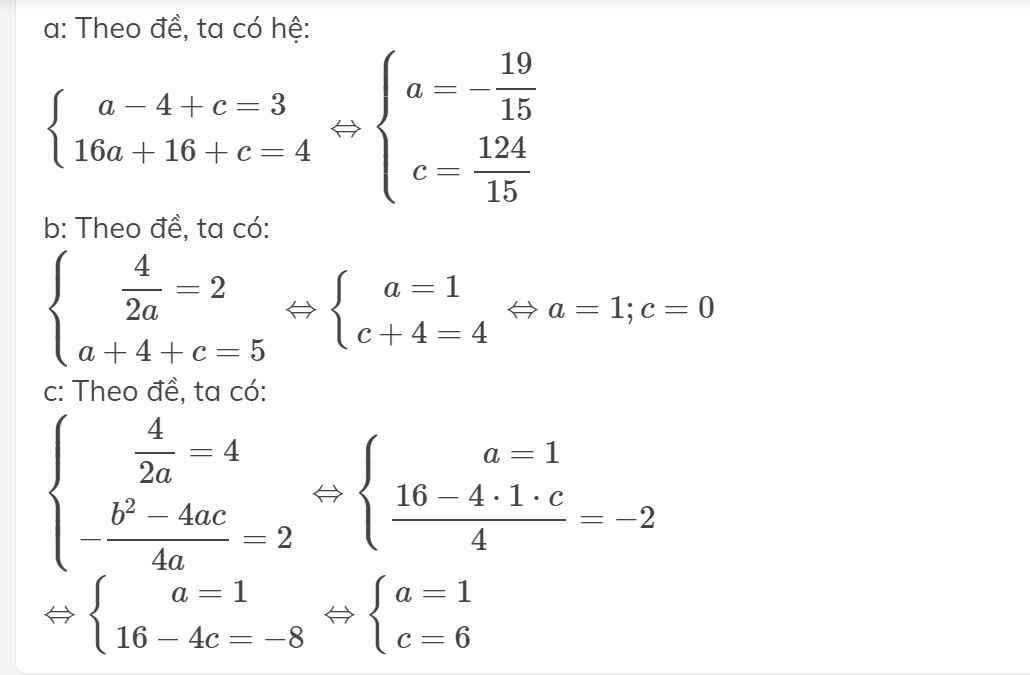Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


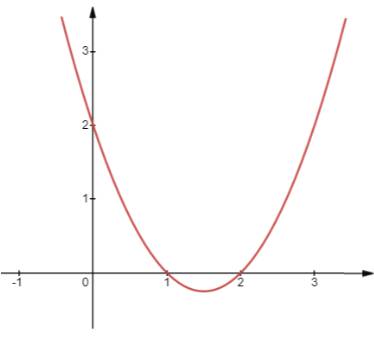
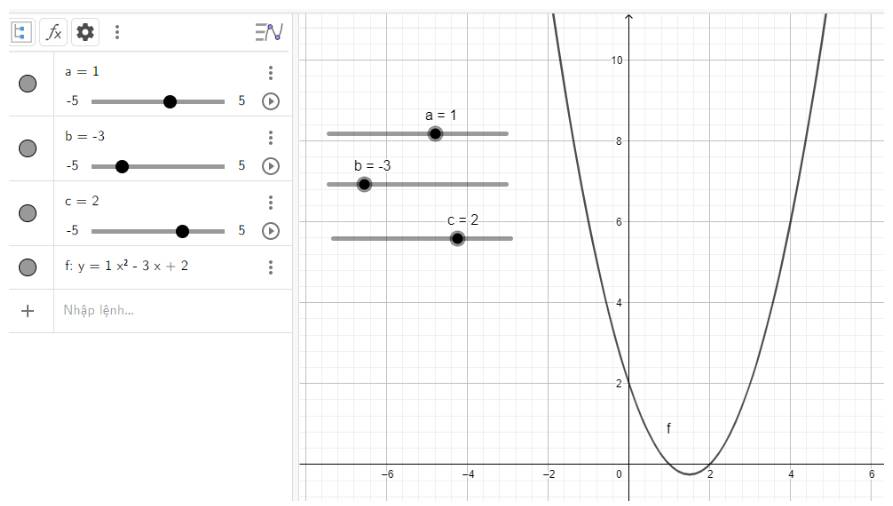
a) Đồ thị \(y = {x^2} - 3x + 2\)
- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;2);(1;0)
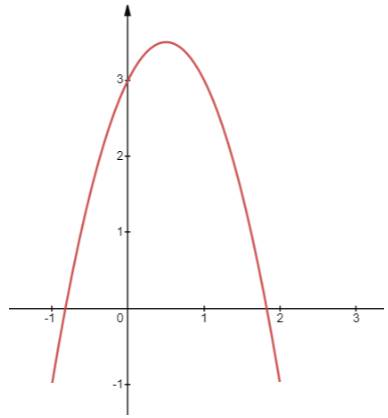
b) Đồ thị \(y = - 2{x^2} + 2x + 3\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 2 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;3);(1;3)
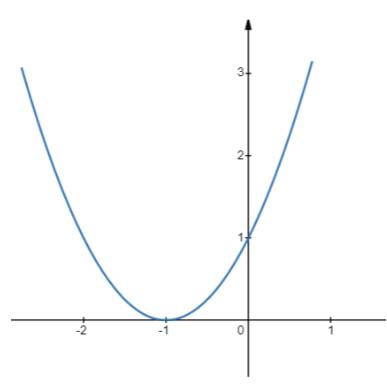
c) Đồ thị\(y = {x^2} + 2x + 1\)
- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x = - 1\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;1); (1;4)
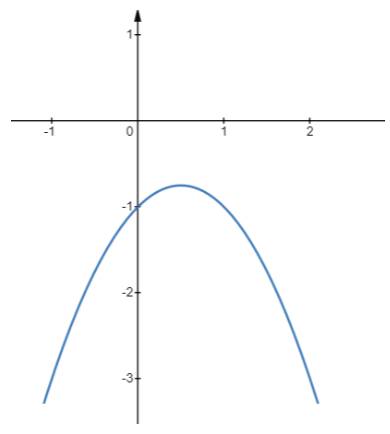
d) Đồ thị \(y = - {x^2} + x - 1\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 1 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;-1); (1;-1)

Lời giải:
Để 2 đths $y=ax+b$ tiếp xúc với cả 2 parabol đã cho thì 2 pt hoành độ giao điểm : \(\left\{\begin{matrix} ax+b=8-3x-2x^2\\ ax+b=2+9x-2x^2\end{matrix}\right.\) đều có nghiệm duy nhất
\(\Leftrightarrow \left\{\begin{matrix} 2x^2+x(a+3)+(b-8)=0(1)\\ 2x^2+x(a-9)+(b-2)=0(2)\end{matrix}\right.\) cả 2 đều có nghiệm duy nhất
Điều này xảy ra khi mà:
\(\Delta_1=(a+3)^2-8(b-8)=0\)
\(\Delta_2=(a-9)^2-8(b-2)=0\)
Trừ theo vế ta thu được \(24a-24=0\Rightarrow a=1\Rightarrow b=10\)
Vậy $(a,b)=(1,10)$

PT hoành độ giao điểm:
\(2x^2+3x-1=x-2\\ \Leftrightarrow2x^2+2x+1=0\\ \Delta=4-8< 0\)
Do đó PT vô nghiệm
Vậy parabol không có giao điểm với đt y=x-2

bài 3:
a: Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}a-4+c=3\\16a+16+c=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{19}{15}\\c=\dfrac{124}{15}\end{matrix}\right.\)
b: Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{4}{2a}=2\\a+4+c=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\c+4=4\end{matrix}\right.\Leftrightarrow a=1;c=0\)
c: Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{4}{2a}=4\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\\dfrac{16-4\cdot1\cdot c}{4}=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\16-4c=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\c=6\end{matrix}\right.\)

Câu a bạn tự vẽ và lập bảng
b/ Có \(I\left(2;-3\right)\Rightarrow\left\{{}\begin{matrix}-\frac{b}{2a}=2\\\frac{-b^2+4ac}{4a}=-3\end{matrix}\right.\)
Vì (P) cắt trục tung tại điểm có tung độ bằng 1=> c=1
\(-\frac{b}{2a}=2\Rightarrow-b=4a\) (1)
\(-b^2+4a=-12a\Leftrightarrow b^2=16a\) (2)
Thay (1) vào (2):
\(b^2=-4b\Leftrightarrow b^2+4b=0\Leftrightarrow\left[{}\begin{matrix}b=0\left(l\right)\\b=-4\end{matrix}\right.\)
\(\Rightarrow b=-4\Rightarrow a=1\)
Vậy (P): \(y=x^2-4x+1\)

b: Để y>0 thì \(-\left(x^2-2x-3\right)>0\)
=>(x-3)(x+1)<0
=>-1<x<3
Để y<0 thì (x-3)(x+1)>0
=>x>3 hoặc x<-1
c: \(y=-\left(x^2-2x-3\right)\)
\(=-\left(x^2-2x+1-4\right)\)
\(=-\left(x-1\right)^2+4\le4\)
Dấu '=' xảy ra khi x=1

Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
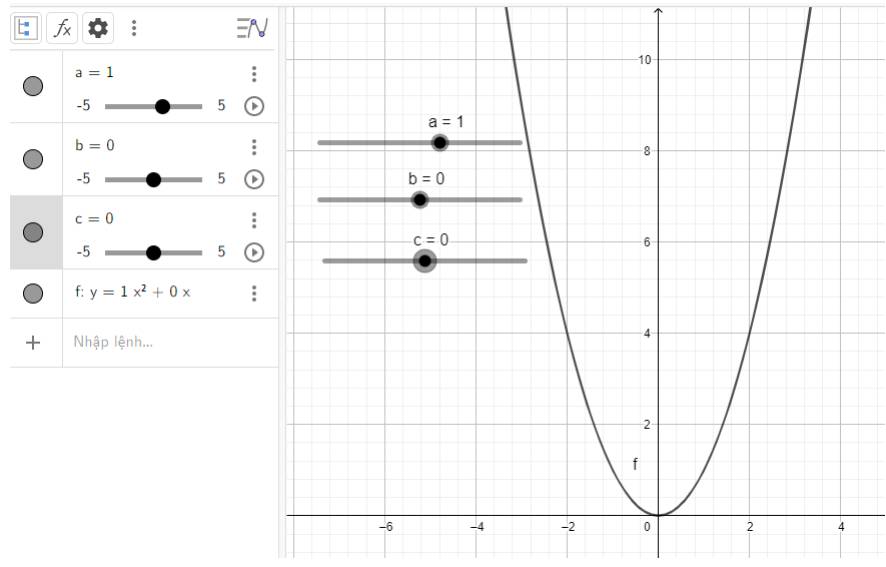
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
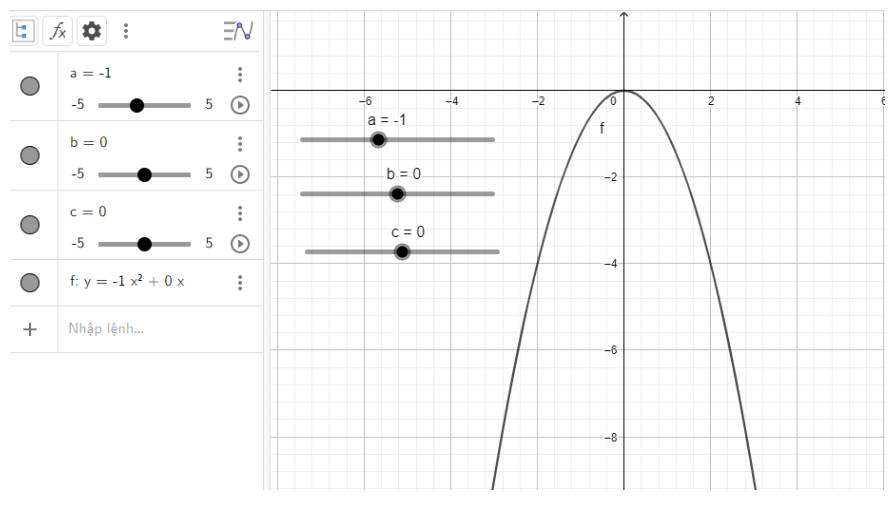
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
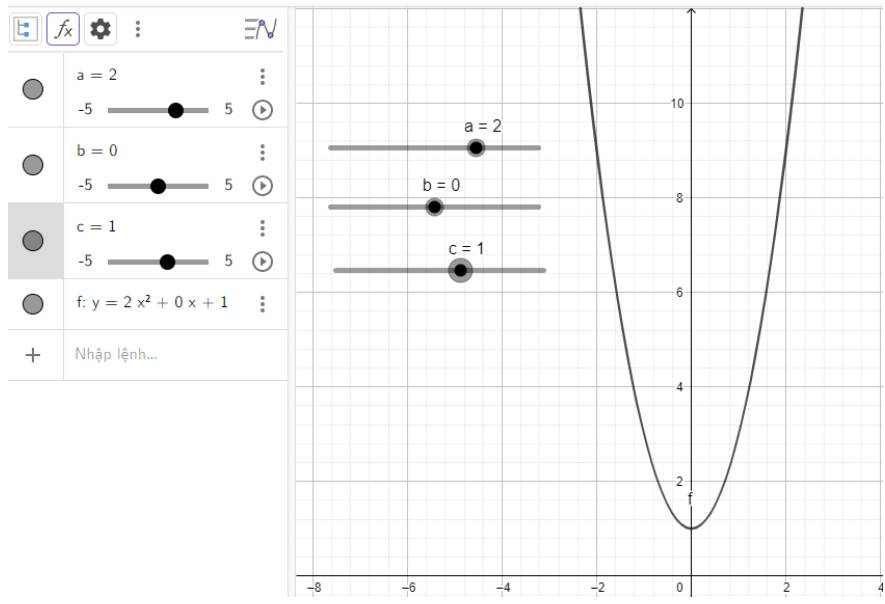
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol