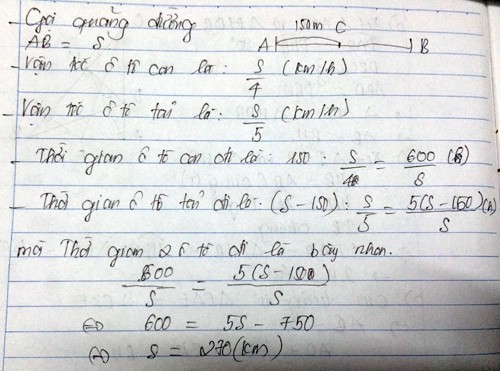Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x và y là vận tốc của xe con và xe tải.
x.4=5.y=AB=> x=5y/4 (1)
Hai ze đi với thời gian như nhau nên (t=S/v)
150/x=(AB-150)/y
<=>AB=(150y/x)+150=5y
<=> 30y+30x=xy (2)
Thay (1) vào (2):
30y+ (30.6y)/4=5y^2/4
<=> 24y+30y=y^2
<=> y(y-54)=0
<=> y=0 (loại)
or y=54=> AB=5.54=270 (km)

Hình minh họa:
A C B ô tô con ô tô tải 150 km
Giải:
Gọi vận tốc của ô tô con và ô tô tải lần lượt là a, b ( a; b > 0 )
Ta có: \(4a=5b\) \(\Rightarrow b=\frac{4}{5}a\)
Theo đề bài, vì số thời gian để di chuyển đến điểm C của 2 xe là như nhau nên:
\(\frac{AC}{a}=\frac{BC}{b}\Rightarrow\frac{150}{a}=\frac{AB-AC}{b}\Rightarrow\frac{150}{a}=\frac{AB-150}{b}\)
\(\Rightarrow150b=a\left(AB-150\right)\)
\(\Rightarrow150.\frac{4}{5}.a=a.AB-150.a\)
\(\Rightarrow120.a=a.AB-150.a\)
\(\Rightarrow120a+150a=a.AB\)
\(\Rightarrow270a=a.AB\)
\(\Rightarrow270a-AB.a=0\)
\(\Rightarrow a\left(270-AB\right)=0\)
Do a > 0 nên:
\(270-AB=0\)
\(\Rightarrow AB=270\)
Vậy quãng đường AB dài 270 km

gọi vận tốc của xe tải là V1, vận tốc của xe taxi là V2
Quãng đường AB là S=V16=V23
=> V1=1/2.V2
thời gian từ lúc khởi hành đến lúc gặp nhau là : t=\(\frac{S}{V1+V2}\)=\(\frac{V2.3}{\frac{1}{2}V2+V2}\)=2 ( giờ )
Vậy : sau 2 giờ 2 xe gặp nhau

gọi quãng đường xe tải và xe con đã đi cho đến khi gặp nhau lần lượt là s1 , s2 ; vận tốc của chúng theo thứ tự là v1 và v2
trong cùng 1 thời gian, quãng đường đi được tỉ lệ thuận với vận tốc nên :
\(\frac{s_1}{v_1}=\frac{s_2}{v_2}=t\)( t chính là thời gian cần tìm )
coi quãng đường AB là đơn vị quy ước thì :
s1 + s2 = 1 ; v1 = \(\frac{1}{6}\); v2 = \(\frac{1}{3}\)do đó t = \(\frac{s_1}{\frac{1}{6}}=\frac{s_2}{\frac{1}{3}}=\frac{s_1+s_2}{\frac{1}{6}+\frac{1}{3}}=\frac{1}{\frac{3}{6}}=2\)
Vậy sau khi khởi hành 2 giờ thì hai xe gặp nhau