Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Chọn C
Khoảng cách giữa vân sáng bậc 2 đến vân sáng bậc 5 ở cùng phía với nhau so với vân sáng trung tâm là 3 mm:
x = x5 - x2 = x2+3 - x3 = 3i
=> i = 1mm
Số vân sáng quan sát được trên vùng giao thoa đối xứng là:
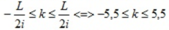
=> Có 11 giá trị của k thỏa mãn
Vậy trên màn có 11 vân sáng

Đáp án D
Khoảng vân là:
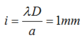
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là :
![]()

Phương pháp: áp dụng công thức tính khoảng vân và công thức xác định vị trí vân sáng
Cách giải: Khoảng vân là: i = λ D a = 1 m m
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là
![]()
Đáp án D

Bạn tham khảo một bài hoàn toàn tương tự như vậy nhé
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24

Cách giải:
Khi dịch chuyển màn ra xa thì khoảng vân sẽ tăng do vậy bậc của vân sẽ giảm xuống, M trở thành vân tối hai lần thì lần cuối cùng ứng với vân tối bậc 4, ta có:
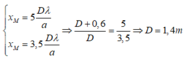
Thay vào phương trình thứ nhất

Đáp án A

Khoảng cách lớn nhất từ giả thiết nghĩa là khoảng cách từ vân sáng bậc 2 (nửa trên) đến vân tối thứ 4 (nửa dưới)
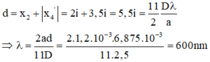
Đáp án D


Cảm ơn bạc Hải Yến. Nhưng mình thấy bạn làm câu a 6i = 12mm => i = 3mm chưa đúng. i = 2mm chứ ?
Bạn ơi. Đề bài của bạn thì dùng ánh sáng đơn sắc để làm thí nghiệm chứ? Câu đầu tiên là giao thoa ánh sáng trắng thì nó không hợp lý lắm.
Mình thì nghĩ là giao thoa ánh sáng đơn sắc.
a) Khoảng cách từ vân sáng bậc 3 bên này đến vân sáng bậc 3 bên kia là 12 mm tức là \(6 i = 12mm \Rightarrow i = 3 mm.\)
=> \(\lambda = \frac{ai}{D} = \frac{0.3.2}{1} = 0,6 \mu m.\)
b) Vị trí vân sáng bậc thứ k là: \(x_ k = k i \)
=> vị trí vân sáng bậc 4 là \(x_4 = 4.i = 4.2 = 8 mm.\)
Vị trí vân tối thứ k+1 là \(x^T_{k+1} = (k+\frac{1}{2})i = \)
=> Vị trí vân tối thứ 5 là: \(x_5^t = (4+0,5).2 = 9 mm.\)
c) Tại M1 thì ta có \(x_M = 7mm. \)
Xét \(\frac{x_M}{i} = 3,5.\) là số bán nguyên => tại M là vân tối.
\(\frac{x_N}{i} = \frac{10}{2} = 5 mm.\) là số nguyên => tại N là vân sáng.