Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Tổng số vân sáng mà hai hệ vân cho được là 33 + 5 = 38
+ Số vân sáng của bức xạ λ 1 cho trên màn
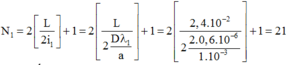
Vậy số vân sáng của bức xạ λ 2 trên màn sẽ là 38 – 21 = 17
→ Tại vị trí biên vân sáng bậc 10 của bức xạ λ 1 trùng với vân sáng bậc 8 của bức xạ λ 2
![]()

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)

Chọn C
Trong bề rộng L=2,4 cm =24 mm có 33 vạch sáng có 5 vạch là kết quả trùng nhau của hai hệ vân nên ta có tổng số vân sáng thực sự do hai bức xạ tạo nên là 33+ 5 =38 vân.
Hai trong 5 vạch trùng nhau nằm ở ngoài cùng của trường giao thoa.
Như vậy ta có: 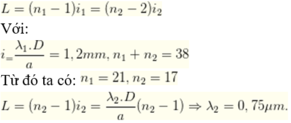

Trên màn có 19 vân sáng, suy ra bề rộng của trường giao thoa là: \(L=18.i\) (*)
Ta có: \(\dfrac{i}{i'}=\dfrac{\lambda}{\lambda'}=\dfrac{0,6}{0,4}=\dfrac{3}{2}\)
\(\Rightarrow i = \dfrac{3}{2}i'\), thay vào (*) ta có:
\(L=27.i'\)
Suy ra trên màn có 28 vân sáng.

Tóm tắt:
\(a=10^{-3}m\)
\(D=0,5m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,6\mu m\)
\(\lambda_3=0,54\mu m\)
\(\lambda_4=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=\)\(k_2\lambda_2=\)\(k_3\lambda_3=\)\(k_4\lambda_4\) \(\Leftrightarrow k_10,64\)\(=k_20,6\)\(=\)\(k_30,54\)\(=k_40,48\)
\(\Leftrightarrow\)\(k_164=k_260=k_354=k_448\) \(\Leftrightarrow\) \(k_164=k_260=k_354=k_448\)
\(\Leftrightarrow k_132=k_230=k_327=k_424\)
BSCNN( 32;30;27;24 ) = 4320
\(k_1=\frac{4320}{32}=135\)
\(k_2=\frac{4320}{30}=144\)
\(k_3=\frac{4320}{27}=160\)
\(k_4=\frac{4320}{24}=180\)
Vậy \(\Delta x=135i_1=144i_2=160i_3=180i_4\)\(=0,0432m=4,32cm\)
\(\rightarrow D\)

Chọn đáp án D
Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒vân trung tâm O là một vân trùng. Tại điểm M ≠O trên màn vân sáng của hai bức xạ trùng nhau thì ta có OM = k 1 i 1 = k 2 i 2 ( k 1 , k 2 nguyên dương)
⇒ k 1 λ 1 = k 2 λ 2 ⇒ k 1 k 2 = λ 2 λ 1 = 5 6 ⇒ k 1 chia hết cho 5, k 2 chia hết cho 6.
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
i’ = k 1 min . i 1 = 5. λ 1 D a = 6 m m , các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm.
Ta có L 2. i ' = 2 , 33
→ số vân trùng của hai bức xạ trên màn bằng n = 2 L 2 i ' + 1 = 2.2 + 1 = 5 vân.

Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒ vân trung tâm O là một vân trùng. Tại điểm M ≠ O trên màn vân sáng của hai bức xạ trùng nhau thì ta có
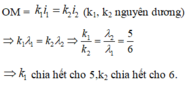
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
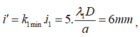
các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm
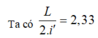
→ số vân trùng của hai bức xạ trên màn bằng
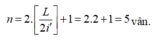
Đáp án A


\(i_1=\dfrac{\lambda_1.D}{a}=1,2mm\)
Số vân sáng của i1 là: \(|\dfrac{24}{2.1,2}|.2+1=21\)
Số vân sáng của i2 là: \(33+5-21=17\)
\(\Rightarrow i_1=1,5mm\)
\(\Rightarrow \lambda_2=0,75\mu m\)
Có thể làm rõ hơn ko ạ???