Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tâm \(I\left(-2;4\right)\) bán kính \(R=\sqrt{5}\)
Thay \(y=0\Rightarrow\left(x+2\right)^2+16=5\Rightarrow\left(x+2\right)^2=-11\) (vô nghiệm)
Vậy Ox không cắt đường tròn
Theo tính chất tiếp tuyến ta luôn có \(IM\perp MA\Rightarrow\Delta IAM\) vuông tại A
Theo Pitago: \(MA^2=IM^2-IA^2=IM^2-R^2\)
Mà \(R=\sqrt{5}\) cố định \(\Rightarrow MA_{min}\) khi \(IM_{min}\)
\(\Rightarrow M\) là hình chiếu vuông góc của I lên Ox \(\Rightarrow M\left(-2;0\right)\)

(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)

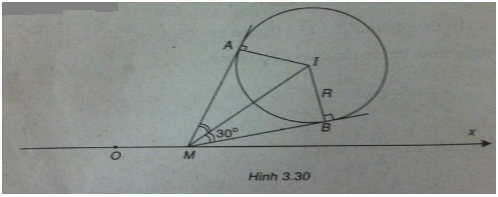
Đường tròn (C) có tâm I (3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\(\Leftrightarrow {x^2} - 6x + 2 = 0\)
\(\Leftrightarrow x = 3 \pm \sqrt 7\)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)

Thay \(y=0\) vào pt (C) ta được: \(\left(x+2\right)^2=-11\) (vô nghiệm)
\(\Rightarrow\)Ox không cắt (C)
Gọi \(I\left(-2;4\right)\) là tâm đường tròn và \(M\left(a;0\right)\)
Theo tính chất tiếp tuyến ta có \(IA\perp MA\Rightarrow\Delta IMA\) vuông tại A
\(\Rightarrow MA=\sqrt{IM^2-IA^2}=\sqrt{IM^2-R^2}\)
\(\Rightarrow MA\) ngắn nhất khi \(IM\) nhỏ nhất \(\Rightarrow M\) là hình chiếu vuông góc của I lên Ox \(\Rightarrow M\left(-2;0\right)\)