Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

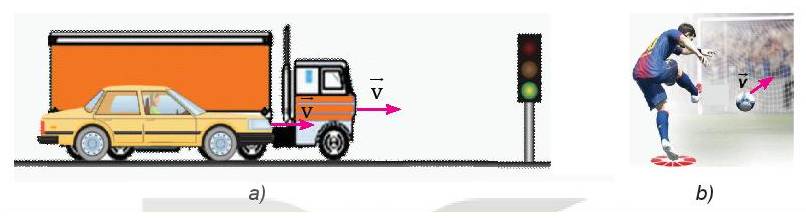
- Hình a: Khi đèn tín hiệu màu đỏ bật sáng thì xe ô tô tải cần phải có một lực hãm lớn hơn xe ô tô con để dừng lại. Ô tô tải có khối lượng lớn hơn nên cần phải có lực hãm lớn hơn để dừng lại so với ô tô con
- Hình b: Vận tốc của quả bóng lớn sẽ khó bắt bóng hơn so với vận tốc của quả bóng nhỏ. Tại vì nếu vận tốc lớn thì quả bóng sẽ bay rất nhanh, thủ môn khó nắm bắt hướng di chuyển của quả bóng.

Tăng tốc độ là sự thay đổi tốc độ của chuyển động từ giá trị nhỏ đến giá trị lớn trong một khoảng thời gian nào đó.

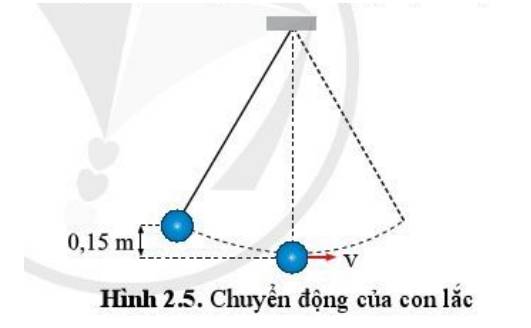
Tốc độ của quả năng lớn nhất thì động năng sẽ lớn nhất
=>Thế năng nhỏ nhất
\(W_{dmax}=W_{tmax}\)
=>\(\dfrac{m\cdot v^2_{Max}}{2}=m\cdot g\cdot h_{max}\)
=>\(v_{Max}=\sqrt{2\cdot g\cdot h_{Max}}\) không phụ thuộc vào khối lượng

1.
Công thức 5.1b: \(v = \frac{{\Delta s}}{{\Delta t}}\)
Tốc độ này được gọi là tốc độ trung bình vì nó cho biết quãng đường vật đi được trong một thời gian xác định.
2.
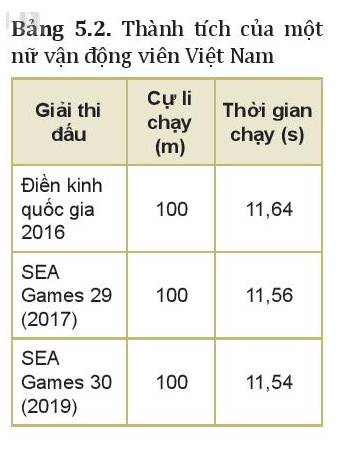
Tốc độ trung bình của nữ vận động viên tại các giải thi đấu là:
- Điền kinh quốc gia 2016:
\(v = \frac{{100}}{{11,64}} = 8,59\left( {m/s} \right) = 30,92\left( {km/h} \right)\)
- SEA Games 29 (2017):
\(v = \frac{{100}}{{11,56}} = 8,65\left( {m/s} \right) = 31,14\left( {km/h} \right)\)
- SEA Games 29 (2019):
\(v = \frac{{100}}{{11,54}} = 8,67\left( {m/s} \right) = 31,21\left( {km/h} \right)\)

1.
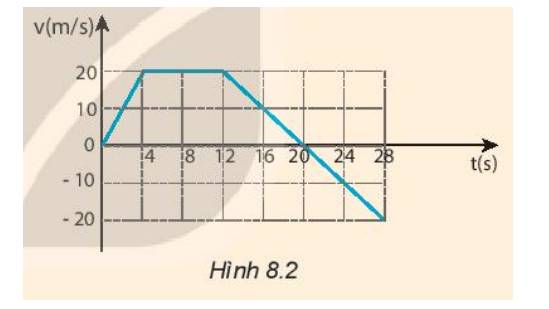
a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s
+ Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\)
+ Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\)
+ Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\)
+ Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\)
b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần.
2.
Gia tốc của con báo là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\)

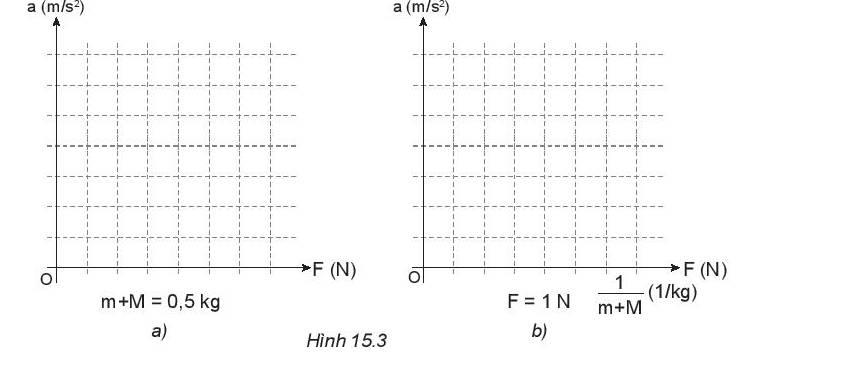
a)
- a phụ thuộc vào F (m + M = 0, 5kg)
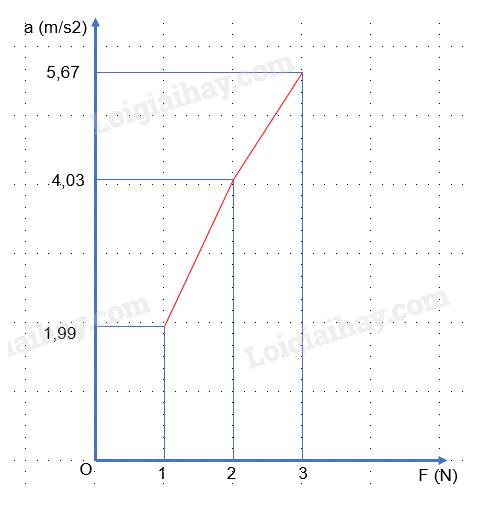
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
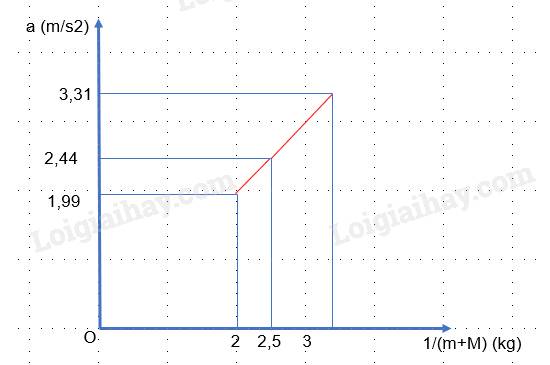
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.







Gọi:
+ Khối lượng, vận tốc trước và sau va chạm của chim đại bàng lần lượt là m1 , v1 , v’1
+ Khối lượng, vận tốc trước và sau va chạm của chim bồ câu lần lượt là m2 , v2 , v’2
Do va chạm của chim đại bàng và chim bồ câu là va chạm mềm nên ta có v’1 = v’2 = v’
Ta có: m1 = 1,8 kg; m2 = 0,65 kg; v1 = 18 m/s; v2 = 7 m/s
Chọn chiều dương là chiều chuyển động của chim đại bàng.
Áp dụng định luật bảo toàn động lượng, ta có:
\(\begin{array}{l}\sum {\overrightarrow {{p_{tr}}} = \sum {{{\overrightarrow p }_s}} } \\ \Leftrightarrow {m_1}.\overrightarrow {{v_1}} + {m_2}.\overrightarrow {{v_2}} = ({m_1} + {m_2}).\overrightarrow {v'} \end{array}\)
Chiếu lên chiều dương, ta có:
\(\begin{array}{l}{m_1}.{v_1} + {m_2}.{v_2} = ({m_1} + {m_2}).v'\\ \Rightarrow v' = \frac{{{m_1}.{v_1} + {m_2}.{v_2}}}{{{m_1} + {m_2}}} = \frac{{1,8.18 + 0,65.7}}{{1,8 + 0,65}} \approx 15,08(m/s)\end{array}\)
Vậy tốc độ của chúng ngay sau khi chim đại bàng bắt được bồ câu là 15,08 m/s.