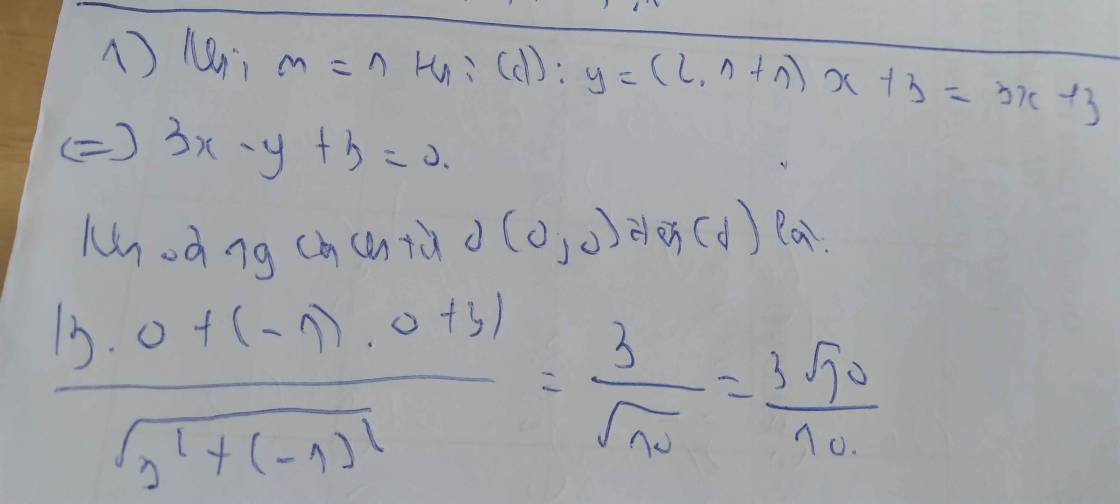Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\left(d\right):y=ax+b\) là đt của (d)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne\sqrt{3}\\b=1\end{matrix}\right.\Leftrightarrow\left(d\right):y=2x+1\Leftrightarrow2x-y+1=0\)
Khoảng cách từ K đến (d) là \(d\left(K;d\right)=\dfrac{6\cdot1-1+1}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)

\(a,\) \(\left(d\right)\) cắt Ox tại A nên \(x=0\Rightarrow y=2\cdot0-2=-2\Rightarrow A\left(0;-2\right)\)
\(\left(d\right)\) cắt Oy tại B nên \(y=0\Rightarrow2x-2=0\Rightarrow x=1\Rightarrow B\left(1;0\right)\)
Từ đó ta được \(OA=2;OB=1\)
Gọi H là chân đường vuông góc từ O đến \(\left(d\right)\)
Áp dụng HTL:
\(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{2}+\dfrac{1}{1}\\ \Rightarrow\dfrac{1}{OH^2}=\dfrac{3}{2}\Rightarrow OH^2=\dfrac{3}{2}\Rightarrow OH=\dfrac{\sqrt{6}}{2}\)
\(b,S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot1\cdot2=1\left(đvdt\right)\)

Phương trình hoành độ giao điểm của (P) và (d):
x2 + 2x -m2 + 1 = 0
Để thỏa mãn yêu cầu bài toán thì pt này phải có hai nghiêm phân biệt xD và xE và xD + xE = 0
Áp dụng định lý Vi-et thì xD +xE = -2 \(\Rightarrow\)m \(\in\varnothing\)

Đáp án:
Giải thích các bước giải:
a) Ta có: 1/OH² = 1/OA² +1/OB² = 1/4+1/1 = 5/4
OH = √4/5
b) đt y= 2x+2
tại x=3 ⇒ y = 4
⇒ I'(3,4)
II' = 4 -2 = 2
tại y=2 ⇒ x = 2
⇒ B'(2,2)
IB' = 3-2= 1
xét Δ IB'I'
1/IH'² = 1/II'² +1/ IB'² = 1/4 +1/1 = 5/4
IH' = √4/5