Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trên tia AB lấy điểm E sao cho AE=AC.
Dễ thấy E nằm giữa A và B vì AB>AC.
Do \(\Delta AMC=\Delta AME\left(c.g.c\right)\Rightarrow ME=MC\)
Lại có:\(AB-AC=AB-AE=EB\)
Ta có:\(MB-MC=MB-ME< EB\)(hệ quả bất đẳng thức tam giác)
\(\Rightarrowđpcm\)

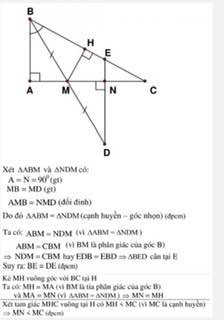
A B C M N H E D I I
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

Đạt ( Quỳnh ) tự vẽ hình nhé !
a) Vì M là trung điểm của Ac
\(\Rightarrow AM=MC=\frac{1}{2}AC\)
Xét \(\Delta ABM\) và \(\Delta CDM\) có :
\(AM=MC\)
\(\widehat{AMB}=\widehat{CMD}\left(đđ\right)\)
\(BM=DM\left(gt\right)\)
Suy ra : \(\Delta ABM=\Delta CDM\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{DCM}=90^o\)
\(\Rightarrow CD\perp AC\)
Vì \(\Delta ABC\) vuông tại A \(\Rightarrow\) BC là cạnh huyền của tam giác
\(\Rightarrow\) BC > AB
Mà \(AB=CD\left(\Delta ABM=\Delta CDM\right)\)
Suy ra : \(BC>CD\)
b ) Tam giác BCD có :
\(BC>CD\Rightarrow\widehat{CDM}>\widehat{CBD}\) ( góc đối diện với cạnh lớn hơn là góc lớn hơn )
Mà \(\widehat{CDM}=\widehat{ABM}\left(\Delta ABM=\Delta CDM\right)\)
Suy ra : \(\widehat{ABM}>\widehat{CBD}\) hay \(\widehat{ABM}>\widehat{MBC}\left(đpcm\right)\)
Chị ấn câu hỏi tương tự nhé
umk. Cảm ơn