Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N H E D I I
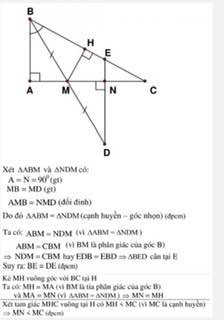
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)

trên cạnh AB lấy điểm E sao cho AE=AC , nối ME
xét tam giác CAM và tam giác EAM có
AE=AC
góc CAM=góc MAE (vì AM là phân giác của góc BAC)
AM là cạnh chung
=> tam giác CAM=tam giác EAM (C.G.C)
=> MC=ME
ta có: gttđ của ME-MB<EC
hay gttđ của MB-MB<EC
mà EC=AB-AE=AB-AC(vì AE=AC)
=>GTTĐ của MB-MC<AB-AC
gttđ là giá trị tuyệt đối nha bạn
Trên tia AB lấy điểm E sao cho AE=AC.
Dễ thấy E nằm giữa A và B vì AB>AC.
Do \(\Delta AMC=\Delta AME\left(c.g.c\right)\Rightarrow ME=MC\)
Lại có:\(AB-AC=AB-AE=EB\)
Ta có:\(MB-MC=MB-ME< EB\)(hệ quả bất đẳng thức tam giác)
\(\Rightarrowđpcm\)