Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là
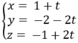
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).
Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0
Suy ra t = 1, do đó H = (2; -4; 1).
Bán kính của (C) bằng
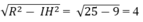

Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
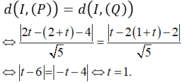
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 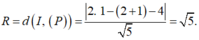
Do đó mặt cầu (S) có phương trình: ![]()

Chọn B
Phương trình (S): x2 + y2 + z2 + 4x - 6y + m = 0 là phương trình mặt cầu <=> m < 13
Khi đó (S) có tọa độ tâm I (-2;3;0) bán kính ![]()
Gọi M (x;y;z) là điểm bất kỳ thuộc Δ.
Tọa độ M thỏa mãn hệ: 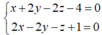
Đặt y = t ta có: 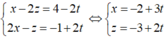
=> Δ có phương trình tham số: 
Δ đi qua điểm N (-2; 0; -3) và có vectơ chỉ phương ![]()
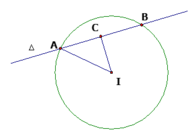
Giả sử mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8. Gọi (C) là đường tròn lớn chứa đường thẳng Δ. Khi đó IC2 = R2 - AC2 = 13 - m - 42 = -m - 3
N (0;-3;-3)

Vậy mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8
<=> -m - 3 = 9 <=> m = -12

Chọn C
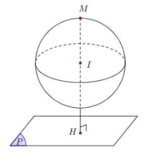
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3

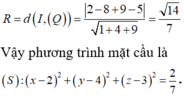






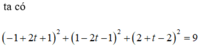
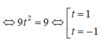
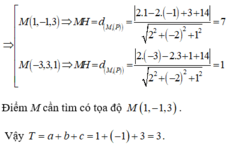

Mặt cầu (S) tâm \(I\left(2;-1;-1\right)\) bán kính \(R=5\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|4-2+1+9\right|}{\sqrt{2^2+2^2+1}}=4\)
Bài toán tương đương với tính thể tích vật thể tròn xoay khi quay miền giới hạn bởi đường tròn \(x^2+y^2=25\) và đường thẳng \(x=4\) quanh trục Ox (phần không chứa tâm đường tròn)
\(\Rightarrow V=\pi\int\limits^5_4\left(25-x^2\right)dx=\dfrac{14\pi}{3}\)