Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) để hàm số : \(y=\dfrac{1-cosx}{sin2x}\) có nghĩa \(\Leftrightarrow sin2x\ne0\Leftrightarrow2x\ne k\pi\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\left(k\in Z\right)\)
vậy tập xác định của hàm số trên là : \(D=R/\left\{\dfrac{k\pi}{2}\backslash k\in Z\right\}\)
b) để hàm số : \(y=\dfrac{tanx}{cosx+1}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\cosx+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\cosx\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k2\pi\\x\ne\pi+k2\pi\end{matrix}\right.\)
vậy tập xác định của hàm số trên là : \(D=R/\left\{\dfrac{\pi}{2}+k2\pi;\pi+k2\pi\backslash k\in Z\right\}\)
b) để hàm số : \(y=\dfrac{1}{sinx}+\dfrac{1}{cosx}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
vậy tập xác định của hàm số trên là : \(D=R/\left\{k\pi;\dfrac{\pi}{2}+k\pi\backslash k\in Z\right\}\)
b) để hàm số : \(y=\sqrt{\dfrac{1}{1-sinx}}\) có nghĩa \(\Leftrightarrow1-sinx>0\)
ta có : \(sinx\le1\forall x\Rightarrow1-sinx\ge0\forall x\) \(\Rightarrow\) hàm số xác định khi \(1-sinx\ne0\) là đủ
\(\Leftrightarrow sinx\ne1\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
vậy tập xác định của hàm số trên là : \(D=R/\left\{\dfrac{\pi}{2}+k2\pi\backslash k\in Z\right\}\)

a/ ĐKXĐ:
\(1-sinx>0\Leftrightarrow sinx\ne1\)
\(\Rightarrow x\ne\frac{\pi}{2}+k2\pi\)
b/ ĐKXĐ:
\(\left\{{}\begin{matrix}sinx.cosx\ne0\\tanx+4cotx+2\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tan^2x+2tanx+4\ne0\left(luôn-đúng\right)\end{matrix}\right.\)
\(\Rightarrow2x\ne k\pi\Rightarrow x\ne\frac{k\pi}{2}\)
c/
\(\left\{{}\begin{matrix}\frac{1-cosx}{2+cosx}\ge0\\2+cosx\ne0\end{matrix}\right.\) \(\Rightarrow x\in R\)

a) \(D=R\backslash\left\{1\right\}\)
b) \(y\left(x\right)\) xác định khi:
\(cos\dfrac{x}{3}\ne0\Leftrightarrow\dfrac{x}{3}\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x\ne\dfrac{3\pi}{2}+k3\pi\)
\(D=R\backslash\left\{\dfrac{3\pi}{2}+k3\pi\right\};k\in Z\)
c) \(y\left(x\right)\) xác định khi:
\(sin2x\ne0\Leftrightarrow2x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\).
\(D=R\backslash\left\{\dfrac{k\pi}{2}\right\};k\in Z\)
d) \(y\left(x\right)\) xác định khi:
\(x^2-1\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\).
\(D=R\backslash\left\{1;-1\right\}\)

a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)
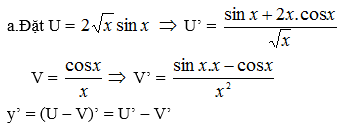
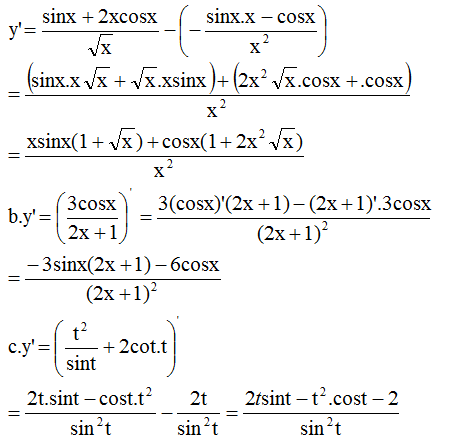
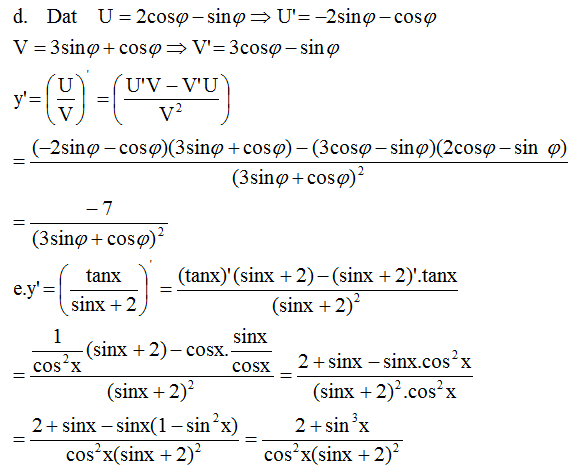
a: \(y=\sin x\cdot\cos x=\dfrac{1}{2}\cdot\sin2x\)
Hàm số này tuần hoàn theo chukì \(\dfrac{2\Pi}{2}=\Pi\)
c: \(\tan2x\) tuần hoàn theo chu kì \(T_1=\dfrac{\Pi}{2}\)
tan x/2 tuần hoàn theo chu kì \(T_2=\Pi:\dfrac{1}{2}=2\Pi\)
Do đó: \(y=\tan2x+\tan\left(\dfrac{x}{2}\right)\) tuần hoàn theo chu kì \(T=BCNN\left(T1;T2\right)=2\Pi\)