Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=1-\dfrac{1}{\left(x-1\right)^2}\)
Tiếp tuyến d tại \(A\left(a;a+1+\dfrac{1}{a-1}\right)\) có dạng:
\(y=\left(1-\dfrac{1}{\left(a-1\right)^2}\right)\left(x-a\right)+a+1+\dfrac{1}{a-1}\)
\(\Leftrightarrow y=\dfrac{a^2-2a}{\left(a-1\right)^2}x+\dfrac{a^2}{\left(a-1\right)^2}\)
\(\Rightarrow M\left(\dfrac{a^2}{2a-a^2};0\right)\) ; \(N\left(0;\dfrac{a^2}{\left(a-1\right)^2}\right)\Rightarrow\left\{{}\begin{matrix}OM=\dfrac{a^2}{\left|2a-a^2\right|}\\ON=\dfrac{a^2}{\left(a-1\right)^2}\end{matrix}\right.\)
\(\dfrac{a^2}{\left(a-1\right)^2}=\dfrac{2a^2}{\left|2a-a^2\right|}\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\\left|a^2-2a\right|=2\left(a^2-2a+1\right)\end{matrix}\right.\)
Đặt \(a^2-2a=t\Rightarrow\left|t\right|=2\left(t+1\right)\) (với \(t\ge-1\))
\(\Leftrightarrow\left[{}\begin{matrix}2t+2=t\\2t+2=-t\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}t=-2\left(loại\right)\\t=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow a^2-2a=-\dfrac{2}{3}\Leftrightarrow a^2-2a+\dfrac{2}{3}=0\)
Người ra đề đam mê với nghiệm xấu thì phải

- Tập xác định: D = R\{-1}.
- Đạo hàm: 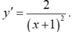
- Đồ thị hàm số cắt trục tung tại điểm A(0; -1).
- Hệ số góc của tiếp tuyến tại điểm A là: k = y’(0) = 2.
Chọn B.

Tập xác định: D = R \{1}.
- Đạo hàm: 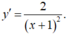
- Đồ thị hàm số cắt trục tung tại điểm A(0; -1)
⇒ y'(0) = 2.
Chọn B.

\(y'=\dfrac{-2}{\left(x-1\right)^2}\)
Gọi điểm trên trục tung có tọa độ \(M\left(0;m\right)\)
Đường thẳng d qua M có dạng: \(y=kx+m\)
d không tiếp xúc đồ thị hàm số khi và chỉ khi:
\(\left\{{}\begin{matrix}\dfrac{x+1}{x-1}=kx+m\\k=\dfrac{-2}{\left(x-1\right)^2}\end{matrix}\right.\) vô nghiệm
\(\Rightarrow\dfrac{x+1}{x-1}=\dfrac{-2x}{\left(x-1\right)^2}+m\) vô nghiệm
\(\Rightarrow\left(m-1\right)x^2-2\left(m+1\right)x+m+1=0\)
\(\Delta'=\left(m+1\right)^2-\left(m-1\right)\left(m+1\right)< 0\)
\(\Leftrightarrow2m+2< 0\)
\(\Rightarrow m< -1\)
Hay \(y< -1\)

Lời giải:
$y'=\frac{-1}{(x+1)^2}$
Giao điểm của đồ thị $y=\frac{x+2}{x+1}$ vớ trục hoành là $(-2,0)$
PTTT của $y=\frac{x+2}{x+1}$ tại điểm tiếp điểm $(-2,0)$ là:
$y=f'(-2)(x+2)+f(-2)=\frac{-1}{(-2+1)^2}(x+2)+0$
$y=-x-2$
Đường tiếp tuyến $y=-x-2$ cắt trục tung tại điểm có tung độ:
$y=-0-2=-2$