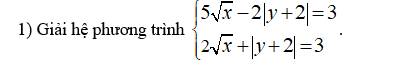KN
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
3
DN
11 tháng 9 2016
1. Cho biểu thức:
A= (x+1/x2+4x+4 - x-1/x2-4)× x×2/3
a. RG A
b. Tính giá trị của A khi |2x-1|=3
c. Tìm giá trị nguyên của x để B=A(x-2) € Z
2. Đường sông từ A→B ngắn hơn đường bộ từ A→B là 10km. Đường đi từ A→B canô hết 3h20', ô tô đi hết 2h. Biết v canô < v ô tô 17km/h. Tính v canô.
3. Giải pt_bất pt:
a. x+3/x+1 + x+5/x =2
b. |2x-7|=4-3x
c. 2(4-2x)+5<=15-5x
d. 1+ x+1/3 > 3x-1/6 -2
4. Cho hv ABCD. Gọi E là 1 điểm € BC qua A kẻ Ax vuông góc với AE cắt CD tại F.
a. CMR:AE=AF
b. Tr.tuyến AI của ▲AEF cắt CD tại K. Qua E kẻ đt // AB cắt AI tại G. CMR: tứ giác EKFG là h.thoi.
c. CMR: AE2= FK.FC
d. CMR: khi E thay đổi trên BC thì P▲EKC ko đổi.
5. Cho a+b+c=1. CMR: a2+b2+c2>=1/3
VN
3
28 tháng 8 2016
Giả sử a < b
Ta có:
a + b < b + b = 2b < a.b ( vì a > 2)
=> a + b < a.b ( đpcm)
S
10 tháng 9 2018
Bài 70:
\(a.\sqrt{\dfrac{25}{81}.\dfrac{16}{49}.\dfrac{196}{9}}=\sqrt{\left(\dfrac{5}{9}\right)^2}.\sqrt{\left(\dfrac{4}{7}\right)^2}.\sqrt{\left(\dfrac{14}{3}\right)^2}=\dfrac{5}{9}.\dfrac{4}{7}.\dfrac{14}{3}=\dfrac{40}{27}\)
\(b.\sqrt{3\dfrac{1}{16}.2\dfrac{14}{25}.2\dfrac{34}{81}}=\sqrt{\dfrac{49}{16}.\dfrac{64}{25}.\dfrac{196}{81}}=\sqrt{\left(\dfrac{7}{4}\right)^2}.\sqrt{\left(\dfrac{8}{5}\right)^2}.\sqrt{\left(\dfrac{14}{9}\right)^2}=\dfrac{7}{4}.\dfrac{8}{5}.\dfrac{14}{7}=\dfrac{196}{45}\)
\(c.\dfrac{\sqrt{640}.\sqrt{34,3}}{\sqrt{567}}=\dfrac{\sqrt{640.34,3}}{\sqrt{567}}=\dfrac{\sqrt{8^2.7^2.7}}{\sqrt{\left(3^2\right)^2.7}}=\dfrac{8.7}{9}=\dfrac{56}{9}\)
\(d.\sqrt{21,6}.\sqrt{810}.\sqrt{11^2-5^2}=\sqrt{21,6.810.\left(11-5\right)\left(11+5\right)}=\sqrt{216.81.16.6}=\sqrt{1296.81.16}=\sqrt{\left(36.9.4\right)^2}=36.9.4=1296\)
SD
2
26 tháng 2 2023
câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)
VD
13 tháng 7 2018
a) Theo hệ thức lượng trong tam giác vuông ta có:
AB.AC=AH.BC
AH^2=AM.AB
AH^2=AN.AC
=> AH^4=AM.AB.AN.AC=AM.AN.BC.AH
<=>AH^3=AM.AN.BC (đpcm)
b) Theo hệ thức lượng trong tam giác vuông ta có:
AH.HB=HM.AB
HN.AC=AH.HC
Tứ giác ANHM vcó 3 góc vuông nên là hình chữ nhật
=> AH=MN; AN=MH;AM=HN
Ta có:
AN.AB + AM.AC
=MH.AB+HN.AC
=AH.BH+AH.HC
=AH(BH+HC)
=AH.BC
=MN.BC
Vậy MN. BC = AN.AB + AM.AC
MD
25 tháng 6 2017
Áp dụng BĐT Cauchy ta có:
P = \(x^2+y^2+\dfrac{33}{xy}\) \(\ge\) \(\dfrac{\left(x+y\right)^2}{2}+\dfrac{33}{x+y}\) = \(\dfrac{4^2}{2}+\dfrac{33}{4}=\dfrac{65}{4}\)
=> Dấu = xảy ra <=> \(\left\{{}\begin{matrix}x+y=4\\x=y\end{matrix}\right.\) <=> \(x=y=2\)
Vậy ...............................
14 tháng 1 2017
coi như giải hệ pt
\(\hept{\begin{cases}y=x+1\left(1\right)\\y^2-3y\sqrt{x}+2x=0\left(2\right)\end{cases}}\)
\(\left(2\right)\Leftrightarrow\left(y^2-3\sqrt{x}.y+\frac{9x}{4}\right)=\frac{9x}{4}-2x=\frac{x}{2}\\ \)
\(\left(y-\frac{3\sqrt{x}}{2}\right)^2=\left(\frac{\sqrt{x}}{2}\right)^2\Rightarrow\orbr{\begin{cases}y=\frac{3\sqrt{x}}{2}-\frac{\sqrt{x}}{2}=\sqrt{x}\\y=\frac{3\sqrt{x}}{2}+\frac{\sqrt{x}}{2}=2\sqrt{x}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=x+1\left(3\right)\\2\sqrt{x}=x+1\left(4\right)\end{cases}}\)
\(\left(3\right)\Leftrightarrow\orbr{\begin{cases}\left(\sqrt{x}-\frac{1}{2}\right)^2=\frac{1}{4}-1\left(vonghiem\right)\\\left(\sqrt{x}-1\right)^2=0\Rightarrow\sqrt{x}=1\Rightarrow x=1\end{cases}}\)
Vậy chỉ có điểm x=1; y=2 thỏa mãn