Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Với a = 4,15 (cm); b = 7,25 (cm), sử dụng máy tỉnh, ta tính được:
BC = 8,35 cm
BD = 3,04 cm
DC ≈ 5,31 cm
AM ≈ 4,18 cm
DM ≈ 1,14cm
Ta có:
\(\widehat{ABC}=\widehat{ADC}\) và AD = BC = b = 7,25cm vì ABCD là hình bình hành.
Xét hai tam giác ADF và CBE ta có:
\(\widehat{ABC}=\widehat{ADC}\) (cmt)
AD = BC (cmt)
\(\widehat{DAF}=\widehat{BCE}\) (2 góc so le trong)
Vậy \(\Delta ADF=\Delta CBE\) (g-c-g).
=> AF = CE.
Cho AF = CE = x.
Áp dụng tính chất của đường phân giác BE trong tam giác ABC ta có:
\(\dfrac{AB}{BC}=\dfrac{AE}{CE}=\dfrac{AF+FE}{CE}\)
=> \(\dfrac{a}{b}=\dfrac{x+m}{x}=>x=\dfrac{mb}{a-b}\)= \(\dfrac{3,45.7,25}{12,5-7,25}=\dfrac{667}{140}\)
=> AC = \(2x+m=2.\dfrac{667}{140}+3,45=\dfrac{1817}{140}\approx12,98\)
Vậy AC \(\approx12,98\) cm.
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: \(\frac{DB}{DC}=\frac{AB}{AC}\)(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
uy ra: \(\frac{DB}{DB+DC}=\frac{15}{15+20}\)(tính chất tỉ lệ thức)
Suy ra: \(\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}cm\)
\(\Rightarrow DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}cm\)
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
Suy ra :\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mà\(\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ADC}}=\frac{3}{4}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = a 2 + b 2
Suy ra: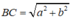
Ta có: AM = BM = 1/2.BC (tính chất đường trung tuyến ứng với cạnh huyền).
Suy ra: AM = 1/2 a 2 + b 2
Vì AD là đường phân giác của ∠(BAC) nên:
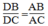(tính chất đường phân giác)
Suy ra: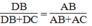 
hay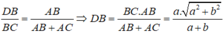 
Vậy
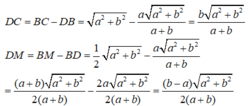
a)
Vậy ∠EBD = 900
Vậy trong hình vẽ có ba tam giác vuông đó là:
∆ABE, ∆CBD, ∆EBD.
b) ∆ABE và ∆CDB có:
∠A = ∠C = 900
∠ABE = ∠CDB
=> ∆ABE ∽ ∆CDB => AB/CD = AE/CB
=> CD = AB.CB/AE
= 18 (cm)
∆ABE vuông tại A => BE =
= 18 cm
∆EBD vuông tại B => ED =
= 28,2 cm
c) Ta có: 
= 1/2 . 10.15 + 1/2 . 12.18
= 75 + 108 = 183 cm2
SACDE = 1/2 (AE + CD).AC =1/2 (10+18).27=378 cm2
=> SEBD = SEBD – ( SABE + SDBC) = 378 – 183 = 195cm2
a) Theo đề bài ta có:
\(\dfrac{AD}{DC}=\dfrac{BA}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
\(\dfrac{AD}{AD+DC}=\dfrac{15}{15+10}hay\dfrac{AD}{AC}=\dfrac{15}{25}\)
=> AD = \(\dfrac{15.AC}{25}=\dfrac{15.15}{25}=9\left(cm\right)\)
DC = AC - AD = 15 - 9 = 6 (cm)
Vậy AD = 9cm; DC = 6cm.
b) Vì BD \(\perp\) BE nên BE là đường phân giác của góc ngoài tại đỉnh B.
Áp dụng tính chất đường phân giác của góc ngoài ta có:
\(\dfrac{EC}{EA}=\dfrac{EC}{EC+AC}=\dfrac{BC}{BA}\)
hay \(\dfrac{EC}{EC+15}=\dfrac{10}{15}=\dfrac{2}{3}\)
=> EC = 30 (cm)
Vậy EC = 30cm.
