Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn lên mạng hoặc vào xem câu hỏi tương tự nha!
Nhớ k mk đấy nha!
thanks nhìu!
OK..OK..OK

a: Xét ΔABC có M,N lần lượt la trung điểm của BA và BC
nên MN là đường trung bình
=>MN//AC và MN=AC/2(1)
Xét ΔADC có Q,P lần lượt là trung điểm của DA và DC
nên QP là đường trung bình
=>QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Suy ra: MQ//NP
b: MN+NP+MQ+PQ
=AC/2+AC/2+BD/2+BD/2
=AC+BD

Xét tứ giác MBAC có góc MBA=góc MCA=góc BMC=90 độ
nên MBAC là hình chữ nhật
=>MA=BC

Ta có
\(MN\perp BC;AB\perp BC\) => MN//AB \(\Rightarrow\frac{MN}{AB}=\frac{CM}{CA}\) (Talet trong tam giác)
\(MP\perp AD;CD\perp AD\) => MP//CD \(\Rightarrow\frac{MP}{CD}=\frac{AM}{CA}\) (Talet trong tam giác)
\(\Rightarrow\frac{MN}{AB}+\frac{MP}{CD}=\frac{CM}{CA}+\frac{AM}{CA}=\frac{CA}{CA}=1\left(dpcm\right)\)

Có MP//BC nên \(\frac{AM}{AB}=\frac{AP}{AC}\Rightarrow AP=\frac{4.8}{6}=\frac{16}{3}\)
NP=AP-AN=16/3-3=?

A B C D N P M
Vì\(\hept{\begin{cases}AB\perp BC\left(\widehat{B}=90^0\right)\\MN\perp BC\left(gt\right)\end{cases}\Rightarrow AB//MN}\)( từ vuông góc đến song song )
Xét tam giác ABC có: \(AB//MN\left(cmt\right)\)
\(\Rightarrow\frac{MN}{AB}=\frac{MC}{AC}\)( hệ quả của định lý Ta-let)
Vì \(\hept{\begin{cases}AD\perp DC\left(\widehat{D}=90^0\right)\\MP\perp AD\left(gt\right)\end{cases}\Rightarrow}MP//DC\)( từ vuông góc đến song song )
Xét tam giác ADC có \(MP//DC\left(cmt\right)\)
\(\Rightarrow\frac{MP}{CD}=\frac{AM}{AC}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{MN}{AB}+\frac{MP}{CD}=\frac{MC}{AC}+\frac{AM}{AC}=\frac{AC}{AC}=1\left(đpcm\right)\)
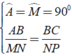
Ta có: Δ MNP ∼ Δ ABC ⇒ MN/AB = NP/BC = MP/AC
Chọn đáp án A.