Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: a+b+c khác 0
\(\frac{a+b-c}{c}=\frac{b+c-a}{a}=\frac{c+a-b}{b}\)
\(\Rightarrow2+\frac{a+b-c}{c}=2+\frac{b+c-a}{a}=2+\frac{c+a-b}{b}\)
\(\Rightarrow\frac{a+b+c}{c}=\frac{a+b+c}{a}=\frac{a+b+c}{b}\)
\(\Rightarrow a=b=c\)
thay a=b=c vào B ta có:
\(B=\left(1+\frac{a}{a}\right)\cdot\left(1+\frac{a}{a}\right)\cdot\left(1+\frac{a}{a}\right)=2\cdot2\cdot2=8\)
TH2: a+b+c=0
=> c=-a-b
=>a=-b-c
=>b=-a-c
thay a,b,c vào B ta có:
\(B=\left(1+\frac{-\left(a+c\right)}{a}\right)\cdot\left(1+\frac{-\left(b+c\right)}{c}\right)\cdot\left(1+\frac{-\left(a+b\right)}{b}\right)\)
\(B=\left(-\frac{c}{a}\right)\cdot\left(-\frac{b}{c}\right)\cdot\left(-\frac{a}{b}\right)=-1\)
p/s: th2 ko chắc nhá

(x-1)200+(y+2)300=0
(x-1)^200 > 0 ; (y+2)^300>0
=> (x-1)^200 = 0 và (y + 2)^300 = 0
=> x - 1 = 0 và y + 2 = 0
=> x = 1 và y = - 2
thay vào rồi tính như bình thường thôi
Vì \(\left(x-1\right)^{200}\ge0\forall x\); \(\left(y+2\right)^{300}\ge0\forall y\)
\(\Rightarrow\left(x-1\right)^{200}+\left(y+2\right)^{300}\ge0\)
mà \(\left(x-1\right)^{200}+\left(y+2\right)^{300}=0\)( giả thiết )
\(\Rightarrow\left(x-1\right)^{200}+\left(y+2\right)^{300}=0\)\(\Leftrightarrow\hept{\begin{cases}x-1=0\\y+2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-2\end{cases}}\)
Thay \(x=1\)và \(y=-2\)vào biểu thức ta được:
\(P=2.1^{100}-5.\left(-2\right)^3+4=2-5.\left(-8\right)+4=2+5.8+4\)
\(=2+40+4=46\)

Q= (x2 - 2y2 + 3/4xy) - (2x2 - y2 + 3/4xy)
Q = x2 - 2y2 + 3/4xy - 2x2 + y2 - 3/4xy
Q= (x2 - 2x2) + (-2y2 + y2) + (3/4xy - 3/4xy)
Q= -x2 - y2
#Hk_tốt
#Ken'z
\(\left(2x^2-y^2+\frac{3}{4}xy\right)+Q=x^2-2y^2+\frac{3}{4}xy\)
\(\Rightarrow Q=x^2-2y^2+\frac{3}{4}xy-2x^2+y^2-\frac{3}{4}xy\)
\(\Rightarrow Q=-x^2-y^2\)
Vậy \(Q=-x^2-y^2\)

Bài 10: Tìm x, y biết: x/y = 2/5 và x + y = 70
Theo bài ra ta có
\(\frac{x}{y}=\frac{2}{5}\Rightarrow\frac{x}{2}=\frac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{70}{7}=10\)
\(\hept{\begin{cases}\frac{x}{2}=10\\\frac{y}{5}=10\end{cases}\Rightarrow\hept{\begin{cases}x=10\\y=50\end{cases}}}\)
Vậy x;y = {10;50}
Bài 13. Mẹ bạn Minh gửi tiền tiết kiệm 2 triệu đồng theo thể thức “có kì hạn 6 tháng”. Hết thời hạn 6 tháng, mẹ Minh được lĩnh cả vốn lẫn lãi là 2 062 400.Tính lãi suất hàng tháng của thể thức gửi tiết kiệm này.
Giải
Số tiền lãi tiết kiệm trog 6 tháng của 2 triệu đồng lak :
2 062 400 - 2 000 000 = 62 400 ( đồng )
Số tiền lãi suất hàng tháng của thể chức gửi tiết kiệm này lak
62 400 : 6 = 10 400 ( đồng )
Vậy ...


16: Tìm nghiệm nguyên của phương trình
x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- )2 = 3 –
Ta thấy (x- )2 = 3 –
≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)

Ta có : \(P\left(x\right)=3x^3-2x+x^2-3x^3+2x^2+3-x\)
\(=-3x+3x^2+3\)
\(Q\left(x\right)=5x^3-x^2-5x^3+4-x^2+2x-2\)
\(=-2x^2+2+2x\)
a, Sắp xếp : \(P\left(x\right)=3x^2-3x+3\)
\(Q\left(x\right)=-2x^2+2x+2\)
b, Ta có : \(A\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\Leftrightarrow A\left(x\right)=3x^2-3x+3-2x^2+2x+2=x^2-x+5\)
Đặt \(x^2-x-5=0\)
\(\Delta=\left(-1\right)^2-4.\left(-5\right)=1+20=21>0\)
Đag nghi vô tỉ thôi KL : vonghiem mà nếu ko phải thì check hộ bài lm tớ ... Dạo này +;- đa thức như đao ý

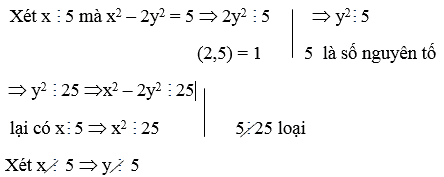
a) ta có: \(\frac{x}{y}=\frac{17}{3}\Leftrightarrow\frac{x}{17}=\frac{y}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{x}{17}=\frac{y}{3}=\frac{x+y}{17+3}=\frac{-60}{20}=-3\)
Do đó:
\(\frac{x}{17}=-3\Rightarrow x=17.\left(-3\right)=-51\)
\(\frac{y}{3}=-3\Rightarrow y=3.\left(-3\right)=-9\)
Vậy ...
b) Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{9}=\frac{y^2}{16}=\frac{x^2+y^2}{25}=\frac{100}{25}=4\)
Do đó:
\(\frac{x^2}{9}=4\Rightarrow x^2=36\Rightarrow x=\pm6\)
\(\frac{y^2}{16}=4\Rightarrow y^2=64\Rightarrow y=\pm8\)
Vậy ...
c) Áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{1+3y}{12}=\frac{1+5y}{5x}=\frac{1+7y}{4x}=\frac{1+3y+17y}{12+4x}=\frac{2\left(1+5y\right)}{2\left(6+2x\right)}=\frac{1+5y}{6+2x}\)
\(\Rightarrow\frac{1+5y}{6+2x}=\frac{1+5y}{5x}\)
\(\Rightarrow6+2x=5x\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
và \(\frac{1+5y}{5x}=\frac{1+7y}{4x}\)
\(\Leftrightarrow\left(1+5y\right).8=\left(1+7y\right).10\)
\(\Rightarrow8+40y=10+70y\)
\(\Rightarrow-2=30y\)
\(\Rightarrow y=-\frac{1}{15}\)
Vậy...
hok tốt!!