Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: chọn ra 4 thầy cô từ 16 thầy cô có ![]() (cách chọn)
(cách chọn)
+ Để chọn được 4 giáo viên phải có cô giáo và đủ ba bộ môn, vậy có các trường hợp sau:
* Trường hợp 1: chọn 2 thầy toán, 1 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 2: chọn 1 thầy toán, 2 cô lý, 1 cô hóa có ![]() (cách chọn)
(cách chọn)
* Trường hợp 3: chọn 1 thầy toán, 1 cô lý, 2 cô hóa có ![]() (cách chọn)
(cách chọn)
Vậy xác suất để chọn được 4 người phải có cô giáo và có đủ ba bộ môn là
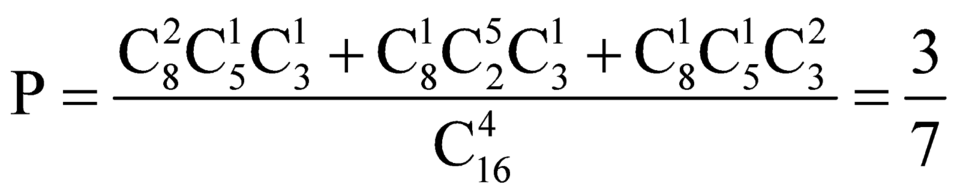

Đáp án D
Một bạn học sinh làm 2 môn sẽ có 36 cách chọn đề, do đó ![]()
Hai bạn Hùng và Vương có chung một mã đề thi thì cùng mã toán hoặc cùng mã tiếng anh do đó ![]()
Vậy xác suất cần tính là 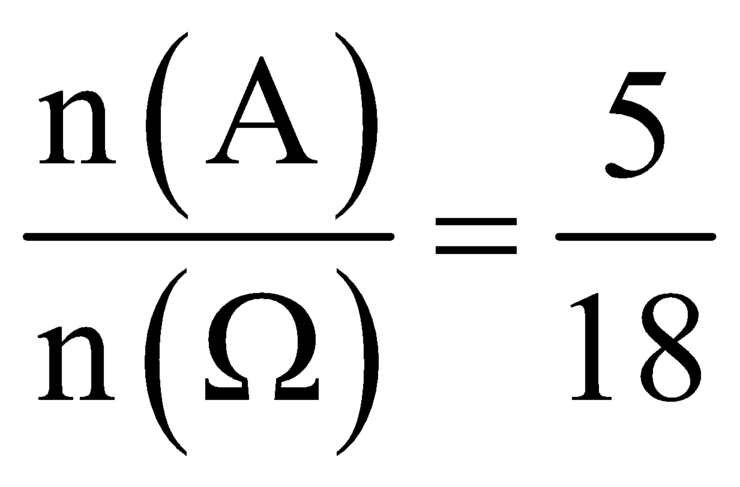

Đáp án D
Không gian mẫu là: Ω = 6 4
TH1: Môn Toán trùng mã đề thi môn Tiếng Anh không trùng có:
Bạn Hùng chọn 1 mã toán có 6 cách và 6 cách chọn mã môn Tiếng Anh khi đó Vương có 1 cách là phải giống Hùng mã Toán và 5 cách chọn mã Tiếng Anh có 6.1.6.5 = 180 cách.
TH2: Môn Tiếng Anh trùng mã đề thi môn Toán không trùng có: 6.1.6.5 = 180 cách.
Vậy P = 180 + 180 6 4 = 5 18

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Chọn C.
Số phần tử của của không gian mẫu: ![]()
- Gọi A là biến cố: “Các giáo viên được chọn có 2 nam và 2 nữ”
![]()
![]()

Với \(n=0\Rightarrow0-0+0-0+0-0=0⋮24\left(đúng\right)\)
Với \(n=1\Rightarrow1-3+6-7+5-2=0⋮24\left(đúng\right)\)
G/s \(n=k\Rightarrow\left(k^6-3k^5+6k^4-7k^3+5k^2-2k\right)⋮24\)
\(\Rightarrow k\left(k^5-3k^4+6k^3-7k^2+5k-2\right)⋮24\\ \Rightarrow k\left(k+1\right)\left(k^2+k+1\right)\left(k^2-k+2\right)⋮24\)
Với \(n=k+1\), ta cần cm \(\left[\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\right]⋮24\)
Ta có \(\left(k+1\right)^6-3\left(k+1\right)^5+6\left(k+1\right)^4-7\left(k+1\right)^3+5\left(k+1\right)^2-2\left(k+1\right)\)
\(=\left(k+1\right)\left[\left(k+1\right)^5-3\left(k+1\right)^4+6\left(k+1\right)^3-7\left(k+1\right)+5\left(k+1\right)-2\right]\\ =\left(k+1\right)\left(k+1-1\right)\left[\left(k+1\right)^2-\left(k+1\right)+1\right]\left[\left(k+1\right)^2-\left(k+1\right)+2\right]\\ =k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)\)
Mà theo GT quy nạp ta có \(k\left(k+1\right)\left(k^2+k+1\right)\left(k^2+k+2\right)⋮24\)
Vậy ta được đpcm



các bạn trả lời nhanh nhé