Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng vân: i = λD/a
Nếu tăng khoảng cách giữa hai khe S1, S2 thì a tăng, i giảm. Do đó số vân trên màn giao thoa tăng.
Chọn đáp án B

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Khi các vân sáng trùng nhau: \(k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
k10,4 = k20,5 = k30,6 \(\Leftrightarrow\) 4k1 = 5k2 = 6k3
BSCNN(4,5,6) = 60
\(\Rightarrow\) k1 = 15 ; k2 = 12 ; k3 = 10 Bậc 15 của \(\lambda_1\) trùng bậc 12 của \(\lambda_2\) trùng với bậc 10 của \(\lambda_3\)
Trong khoảng giữa phải có: Tổng số VS tính toán = 14 + 11 + 9 = 34
Ta xẽ lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_2:\) \(\frac{k_1}{k_2}=\frac{\lambda_1}{\lambda_2}=\frac{5}{4}=\frac{10}{8}=\frac{15}{12}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k2 = 12 thì có tất cả 4 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 5 ; k2 = 4
Vị trí 3: k1 = 10 ; k2 = 8 => Trong khoảng giữa có 2 vị trí trùng nhau.
Vị trí 4: k1 = 15 ; k2 = 12
- Với cặp\(\lambda_2;\lambda_3:\) \(\frac{k_2}{k_3}=\frac{\lambda_3}{\lambda_2}=\frac{6}{5}=\frac{12}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k2 = 12 ; k3 = 10 thì có tất cả 3 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k2 = 6 ; k3 = 5 \(\Rightarrow\) Trong khoảng giữa có 1 vị trí trùng nhau.
Vị trí 3: k2 = 12 ; k3 = 10
- Với cặp \(\lambda_1;\lambda_3:\) \(\frac{k_1}{k_3}=\frac{\lambda_3}{\lambda_1}=\frac{3}{2}=\frac{6}{4}=\frac{9}{6}=\frac{12}{8}=\frac{15}{10}\)
Như vậy: Trên đoạn từ vân VSTT đến k1 = 15 ; k3 = 10 thì có tất cả 6 vị trí trùng nhau
Vị trí 1: VSTT
Vị trí 2: k1 = 3 ; k3 = 2
Vị trí 3: k1 = 6 ; k3 = 4
Vị trí 4: k1 = 9 ; k3 = 6 \(\Rightarrow\) Trong khoảng giữa có 4 vị trí trùng nhau.
Vị trí 5: k1 = 12 ; k3 = 8
Vị trí 6: k1 = 15 ; k3 = 10
Vậy tất cả có 2 + 1 +4 = 7 vị trí trùng nhau của các bức xạ.
Số VS quan sát được = Tổng số VS tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng.
\(\rightarrow D\)



Từ (1); (2); (3) ta được tỷ lệ trên
Số vân sáng đơn sắc cần tìm là
![]() =16
=16

Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)

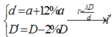
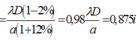

- Khoảng vân: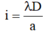
- Nếu tăng khoảng cách giữa hai khe S1, S2 thì a tăng, i giảm. Do đó số vân trên màn giao thoa tăng.