Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải :
Biểu diễn trên đường tròn lượng giác ta có: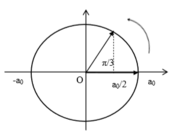
Góc quét được α = π/3
=> Thời gian ngắn nhất để vật đi từ vị trí có gia tốc cực đại đến vị trí gia tốc bằng một nửa gia tốc cực đại là :
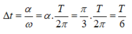

Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
M N x 60 0
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s

Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
M N x 60 0
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s

Chọn đáp án D
Tốc độ bằng một nửa tốc độ cực dại có li độ tương ứng: x = 3 2 A
→ Thời gian ngắn nhất vật đi từ x = 0 đến x = 3 2 A là: Δ t = T 6

Đáp án A
+ Tốc độ bằng một nửa tốc độ cực đại có li độ tương ứng
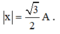 .
.
→ Thời gian ngắn nhất vật đi từ x=0 đến
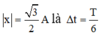

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)
Khoảng thời gian ngắn nhất để vật đi từ vị trí có gia tốc cực đại đến vị trí có gia tốc bằng một nửa gia tốc cực đại là ∆ t = T 6
Đáp án C