Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AD//BC
AE//BC
mà AD và AE có điểm chung là A
nên A,D,E thẳng hàng
b: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)(định lí tổng ba góc trong một tam giác)

Bai 3 :
N M P 20 25
Áp dụng định lí Py - ta - go vào \(\Delta MNP\)vuông tại N:
MP2 = NP2 + MN2
252 = NP2 + 202
=> NP2 = 625 - 400
=> NP2 = 225
=> NP = 15
Bài 3 :
D E F
Ta có :
EF2 = 262 = 676
DE2 + DF2 = 102 + 242 = 676
=> EF2 = DE2 + DF2
Vậy \(\Delta EDF\) là tam giác vuông tại D

Biểu diễn các điểm trên hệ trục tọa độ Oxy ta được:
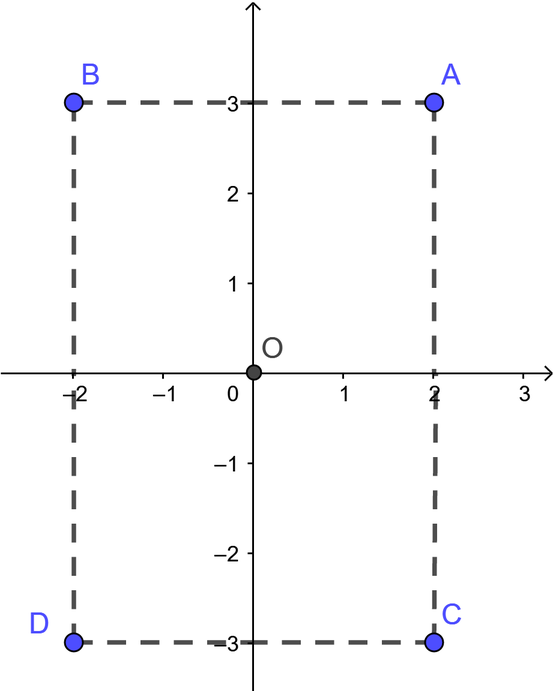
Quan sát hình vẽ ta thấy đoạn AB và CD song song với trục hoành
Chọn đáp án C

a) Xét \(\Delta MNK\) có ND là phân giác ; ND là đường cao ( \(ME\perp ND\) )
\(\Rightarrow\) \(\Delta MNK\) cân tại N
b) Vì \(\Delta MNK\) cân tại N => MN = KN
Xét \(\Delta MND\) và \(\Delta KND\) có :
\(\widehat{MND}=\widehat{KND};MN=KN;ND:chung\)
\(\Rightarrow\) \(\Delta MND\) = \(\Delta KND\)
\(\Rightarrow\widehat{NMD}=\widehat{NKD}=90^o\) hay \(DK\perp NP\) và MD = DK
c) Vì MD = DK suy ra \(\Delta MDK\) cân
\(\Rightarrow\widehat{DMK}=\widehat{DKM}\)
mà \(\widehat{HMK}=\widehat{DKM}\) ( vì cùng phụ với \(\widehat{MKH}\) )
\(\Rightarrow\widehat{DMK}=\widehat{HMK}\) hay Mk là phân giác \(\widehat{HMD}\)
d) Vì \(\)\(\Delta MDK\) cân mà DE là đường cao => DE là trung tuyến=> ME = EK
=> \(\Delta MIK\) cân ( vì IE là đường cao ; trung tuyến )
=> \(\widehat{IMK}=\widehat{MKI}\) mà \(\widehat{IMK}=\widehat{KMP}\)
=> \(\widehat{MKI}=\widehat{KMP}\) mà 2 góc này nằm ở vị trí so le trong
=> IK // MD hay IK // MP
Nhận thấy các đường thẳng song song với trục hoành là MN và PQ.
Vậy chọn đáp án C.