Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

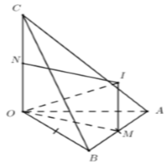
Tứ diện OABC có OA, OB, OC đôi một vuông góc.
Gọi M, N lần lượt là trung điểm của AB và OC
Ta có
Qua M dựng đường thẳng song song với OC, qua N dựng đường thẳng song song với OM. Hai đường thẳng này cắt nhau tại I.
∆ O A B vuông tại O ⇒ M là tâm đường tròn ngoại tiếp I ∈ I N ⇒ I O = I C ⇒ I O = I A = I B = I C ⇒ I là tâm mặt cầu ngoại tiếp O.ABC.
Ta có:
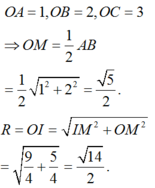
Chọn D.

Bài 1 :Diện tích hình tròn bằng bình phương bán kính nhân với Pi. Như vậy, nếu đường kình giảm 50% thì bán kính giảm 50%. Khi đó diện tích sẽ bằng: 50% bán kính( nhân) 50% bán kính (nhân) Pi= 25% bán kính nhân Pi= 25% diện tích hình tròn ban đầu. Như vậy diện tích hình tròn giảm đi: 100%-25%= 75%
Bài 2 : Diện tích hình tròn = Số Pi x R^2
1. Lúc chưa tăng bán kính lên 10% thì:
S(1) = Pi x R^2
2. Khi tăng bán kính lên 10% thì:
S(2) = Pi x (110%. R)^2
S(2) = Pi x (1,1.R)^2
S(2) = Pi x 1,21.R^2
3. Diện tích hình tròn tăng lên là:
S(2) - S(1)
= (Pi x 1,21.R^2) - (Pi x R^2)
= (1,21 x Pi x R^2) - (1 x Pi x R^2)
= (Pi x R^2) x (1,21 - 1)
= 0,21 x Pi x R^2
Mà:
S(1) = Pi x R^2
Nên diện tích tăng lên là: 0,21 x S(1)
Hay nói cách khác là tăng lên 21%
Đáp số: 21%

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)



Đáp án là C