Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có
AB → = 0 ; 0 ; − 4 ; AC → 1 ; 0 ; − 4 ; BC → 1 ; 0 ; 0 , BD → 0 ; 1 ; 0 , CD → = − 1 ; 1 ; 0
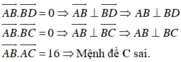

Đáp án B
M(a;b;1) thuộc mặt phẳng (P): 2x – y + z – 3 = 0 => 2a – b + 1 – 3 = 0 => 2a – b – 2 = 0

Đáp án A.
Ta có S : x + a 2 2 + y + b 2 2 + z + c 2 2 = a 2 + b 2 + c 2 4 - d có I - a 2 ; - b 2 ; - c 2
Vì I ∈ d ⇒ I 5 + t ; - 2 - 4 t ; - 1 - 4 t và (S) tiếp xúc với (P) nên d I ; P = R
3 . 5 + t - - 2 - 4 t - 3 . - 1 - 4 t - 1 3 2 + - 1 2 + - 3 2 = 19 ⇔ t + 1 = 1 ⇔ [ t = 0 t = 2
⇒ [ I ( 5 ; - 2 ; - 1 ) I ( 3 ; 6 ; 7 ) ⇒ [ a , b , c , d = - 10 ; 4 ; 2 ; 47 a , b , c , d = - 6 ; - 12 ; - 14 ; 75
Thử lại với a 2 + b 2 + c 2 4 - d = R 2 = 19 thì chỉ có trường hợp {-6;-12;-14;75} thỏa

Đáp án B
Phương pháp: (P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
TH2: I ∈ (P), với I là trung điểm của BC
Cách giải:
Ta có: ![]()
(P) cách đều B, C ó d(B;(P)) = d(c;(P))
TH1: BC // (P)
![]()
=> (P) đi qua O và nhận ![]() là 1 VTPT
là 1 VTPT
![]()
TH2: I ∈ (P) với I là trung điểm của BC
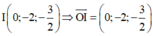
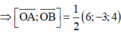
=> (P): 6x – 3y + 4z = 0
Dựa vào các đáp án ta chọn được đáp án B

Chọn C
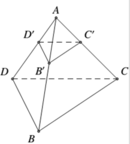
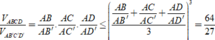
![]()
Dấu = xảy ra khi:![]()
Suy ra 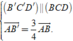
Ta có 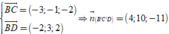
Mặt khác
![]()
Vậy phương trình mặt phẳng (B' C' D') là ![]()
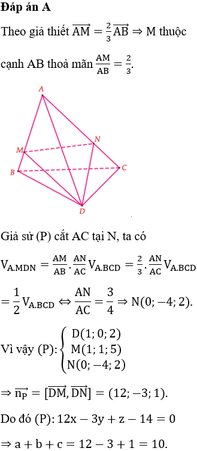
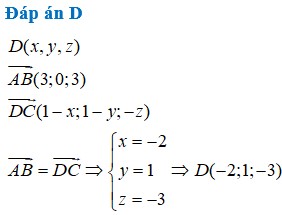

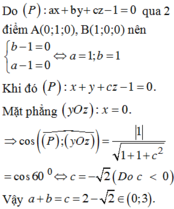
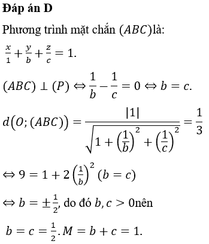
Đáp án D.
Ta có A B → = 0 ; 0 ; − 4 , B C → = 1 ; 0 ; 0 , B D → = 0 ; 1 ; 0 , C D → = − 1 ; 1 ; 0 , A C → = 1 ; 0 ; − 4 . Rõ ràng A B → . B C → = A B → . B D → = A B → . C D → = 0 , nên suy ra D sai.