Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
Thay tọa độ các điểm vào phương trình đường thẳng và kiểm tra tọa độ đó có thỏa mãn phương trình hay không.
Cách giải
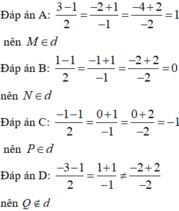

Đáp án C
Gọi B 2 + t ; - 1 - t ; 1 + t A B ¯ = 1 + t ; - t ; t - 2 . Cho A B ¯ . u d ¯ = 0 ⇔ t + 1 - 4 t - 2 t + 4 = 0 ⇔ t = 1 ⇒ A B ¯ = 2 ; - 1 ; - 1
Khi đó d : x - 1 2 = y + 1 - 1 = z - 3 - 1 .

Chọn A
Tìm giao điểm I từ hệ phương trình đường thẳng d và mặt phẳng (P). Viết phương trình đường thẳng IM. Gọi tọa độ điểm M theo tham số của đường thẳng IM rồi xác định tham số đó từ phương trình I M = 4 14

Đáp án D
Phương pháp: △ ⊥ d △ ⊥ A B ⇒ u △ → = u d → ; A B →
Viết phương trình đường thẳng biết điểm đi qua và VTCP.
Cách giải: d; x + 1 - 2 = y - 2 1 = z - 3 3 có 1 VTCP u → - 2 ; 1 ; 3 ; A B → = - 2 ; 3 ; 2
∆ vuông góc với d và AB => AB nhận u → - 2 ; 1 ; 3 và A B → = - 2 ; 3 ; 2 là cặp VTPT
=> ∆ có 1 VTCP v → = A B → ; u → = ( 7 ; 2 ; 4 )
Phương trình đường thẳng ∆: x - 1 7 = y + 1 2 = z - 1 4

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
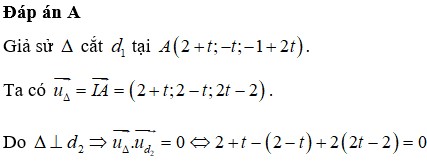


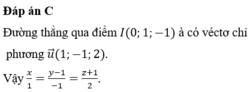

Chọn đáp án A