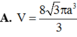Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác \(PBC\)và tam giác \(PAB\)có:
\(\frac{PB}{PA}=\frac{BC}{AB}=\frac{PC}{PB}=\sqrt{2}\)
suy ra \(\Delta PBC~\Delta PAB\left(c.c.c\right)\)
suy ra \(\widehat{PBC}=\widehat{PAB}\).
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}\)
\(=180^o-45^o-135^o\)

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

1.
\(V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}.a.a.2a=\frac{a^3}{3}\)
2.
\(V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.2a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{2}\)
P/s: chóp này là chóp "có đáy là tam giác đều" chứ không phải "chóp tam giác đều"
Hai loại này khác xa nhau đấy, ko lộn xộn nhầm lẫn được đâu
3.
Câu này đề sai
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow SC>SA\) (cạnh huyền luôn lớn hơn cạnh góc vuông)
Do đó đề cho \(SA=SC\) là vô lý
4.
\(AC=BD=\sqrt{AB^2+AD^2}=2a\)
\(\widehat{SCA}=60^0\Rightarrow SA=SC.tan60^0=2a\sqrt{3}\)
\(V=\frac{1}{3}SA.AB.AD=\frac{1}{3}.2a\sqrt{3}.a.a\sqrt{3}=2a^3\)

9.
\(R=\frac{AB}{2}=\frac{a}{2}\) ; \(l=AB=a\)
\(h=\sqrt{l^2-R^2}=\frac{a\sqrt{3}}{2}\)
Thể tích chóp:
\(V=\frac{1}{3}\pi R^2h=\frac{\sqrt{3}}{6}\pi a^3\)
10.
Gọi thiết diện là tam giác ABC vuông cân tại A
\(BC=a\Rightarrow R=\frac{BC}{2}=\frac{a}{2}\)
\(l=AB=\frac{BC}{\sqrt{2}}=\frac{a\sqrt{2}}{2}\)
\(S_{xq}=\pi Rl=\frac{\sqrt{2}}{4}\pi a^2\)
6.
\(l=BC=\sqrt{AB^2+AC^2}=2a\)
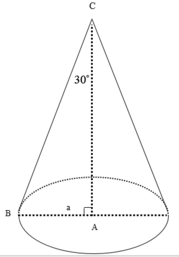
7.
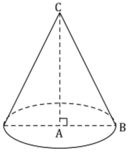
\(h=AC=\frac{AB}{tan30^0}=a\sqrt{3}\) ; \(R=AB=a\)
\(V=\frac{1}{3}\pi R^2h=\frac{\sqrt{3}}{3}\pi a^3\)
8.
Gọi O là tâm đáy
\(\Rightarrow R=OB=\frac{2}{3}.\frac{BC\sqrt{3}}{2}=\frac{BC\sqrt{3}}{3}=a\sqrt{3}\)
\(l=AB=3a\)
\(S_{xq}=\pi Rl=3\sqrt{3}\pi a^2\)


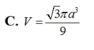
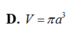
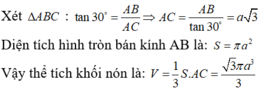
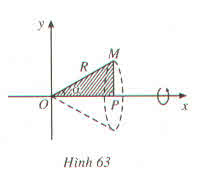
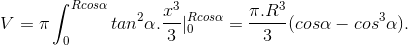
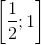 . (vì α ∈
. (vì α ∈ 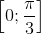 ), α = arccos t.
), α = arccos t.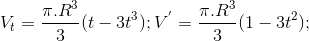
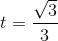
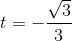 (loại).
(loại).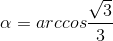 .
.