
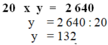
20 x y = 2 640
">Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

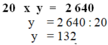

12y + 13y =9000
25y=9000
y=360
123y - 88y=70350
35y=70350
y=2010
Học tốt !!

Ta chứng minh \(P\ge\frac{25}{64}\). Thật vậy:
Đặt \(p=x+y+z=\frac{3}{2},q=ab+bc+ca,r=abc\)
Cần chứng minh:
Dễ thấy khi r giảm thì f(r) giảm. Mà theo Schur: -3/8 + (2*q)/3=-1/9*p^3 + 4/9*q*p <= r
Nên \(f\left(r\right)\ge f\left(\frac{2q}{3}-\frac{3}{8}\right)=\frac{\left(4q-3\right)\left(q-6\right)}{9}\ge0\)
Done.
Bunyakovski hả?
Có: \(\left(x^3+y^3+z^3\right)\ge\frac{\left(x^2+y^2+z^2\right)^2}{x+y+z}=\frac{2\left(x^2+y^2+z^2\right)^2}{3}\)
Cần chứng minh: \(\frac{2\left(x^2+y^2+z^2\right)^2}{3}+x^2y^2z^2\ge\frac{25}{64}\)
Or \(\frac{\left(x^2+y^2+z^2\right)^2}{x+y+z}+\left(x^2y^2z^2+\frac{1}{64}\right)\ge\frac{13}{32}\)
Or: \(\frac{\left(x^2+y^2+z^2\right)^2}{x+y+z}+\frac{1}{4}xyz\ge\frac{13}{32}=\frac{13}{108}\left(x+y+z\right)^3\)(*)
(1)
Điều thú vị là BĐT (*) đúng với mọi x,y,z thuộc R thỏa mãn x + y + z \(\ge0\) (nhờ đẳng thức (1) ).
Mà điều này luôn đúng do điều kiện...

\(y.\frac{52}{26}=\frac{17}{13}\)
\(y=\frac{17}{13}:\frac{52}{26}\)
\(y=\frac{17}{26}\)
\(4\frac{1}{2}:y=\frac{2}{7}\)
\(\frac{9}{2}:y=\frac{2}{7}\)
\(y=\frac{9}{2}:\frac{2}{7}\)
\(y=\frac{63}{4}\)

a, 75 x x = 1800 x = 1800 : 75 x = 24 c, x x 405 = 86265 x = 86265 : 405 x = 213 Đây nha em.
a, 75 x X = 1800
x= 1800:75
x= 24
b, 1855:X = 35
x=1855:35
x =53


18/27=2/3(ta thấy:27:3=9 ,vậy ở tử số ta có:2x9=18)
35/49=10/14
