Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.
xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC
xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42
a) Cần biết ít nhật ba trong năm đại lượng u1, n, d, un, Sn thì có thể tính được hai đại lượng còn lại.
b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.
b1) Biết u1 = -2, un = 55, n = 20. Tìm d, Sn
Áp dụng công thức d =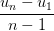 
, Sn =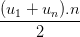 
Đáp số: d = 3, S20 = 530.
b2) Biết d = -4, n = 15, Sn = 120. Tìm u1, un
Áp dụng công thức un = u1 + (n - 1)d và Sn = ,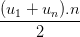
ta có: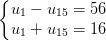 
Giải hệ trên, ta được u1 = 36, u15 = - 20.
Tuy nhiên, nếu sử dụng công thức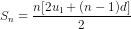 
thì S15 = 120 = 15u1 +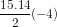 
.
Từ đó ta có u1 = 36 và tìm được u15 = - 20.
b3) Áp dụng công thức un = u1 + (n - 1)d, từ đây ta tìm được n; tiếp theo áp dụng công thức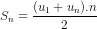 
. Đáp số: n = 28, Sn = 140.
b4) Áp dụng công thức 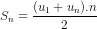, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: u1 = -5, d= 2.
b5) Áp dụng công thức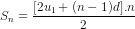 
, từ đây tìm được n, tiếp theo áp dụng công thức un = u1 + (n - 1)d. Đáp số: n = 10, un = -43
Đáp án A
Bạn Nam chọn 3 trong 10 câu nên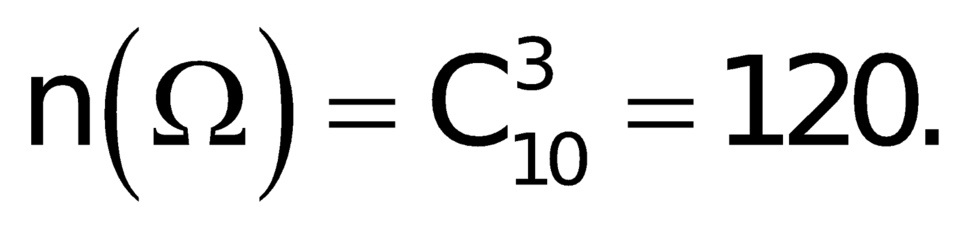
Gọi A là biến cố “Nam chọn ít nhất một câu hình học”.
Khi đó
: “Nam không chọn được câu hình học nào” hay Nam chỉ chọn toàn câu đại số