Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều (+) là chiều chuyển động của vật.
Vật được kéo trên mặt phẳng nằm ngang \(\Rightarrow N=P=mg=15.10=150\left(N\right)\)
Lực ma sát \(F_{ms}=\mu N=0,05.150=7,5\left(N\right)\)
Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\) (1)
Chiếu (1) lên phương chuyển động của vật, ta có:
\(F_k-F_{ms}=ma\Rightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{45-7,5}{15}=2,5\left(m/s^2\right)\)
Vậy gia tốc của thùng là \(2,5m/s^2\).

Tóm tắt:\(m=500kg;F_k=500N;\mu=0,04;t=10s;g=10\)m/s2
\(v=?\)
Bài giải:
Vật kéo theo phương ngang chịu tác dụng của lực kéo và lực ma sát.
Lực ma sát: \(F_{ms}=\mu mg=0,04\cdot500\cdot10=200N\)
Chọn chiều dương là chiều chuyển động vật.
\(\Rightarrow m\cdot a=F_k-F_{ms}=500-200=300N\)
\(\Rightarrow a=\dfrac{300}{500}=0,6\)m/s2
Vật bắt đầu chuyển động \(\left(v_0=0\right)\) sau 10s đạt vận tốc:
\(v=v_0+at=0+0,6\cdot10=6\)m/s

a. Tính vận tốc của vật sau 2s kể từ khi bắt đầu chuyển động.
Vận tốc đầu tiên của vật khi bắt đầu kéo là F/m.
Sau 2s, lực F ngừng tác dụng và vật sẽ bị ma sát. Do đó, vận tốc mới của vật sẽ giảm dần trong thời gian.
Vận tốc cuối cùng của vật khi dừng lại là:
vận tốc = sqrt((F/m)^2 - (2g(2m/s^2)) / m)
Như vậy, ta đã tính được vận tốc của vật sau 2s kể từ khi bắt đầu chuyển động.
b. Sau đó, lực F ngừng tác dụng. Tính quãng đường vật đi tiếp cho tới lúc dừng lại.
Để tính quãng đường, ta sử dụng công thức:
quãng đường = 1/2 * m * vận tốc^2 / g
Ta thuật toán hóa công thức để tính quãng đường.
Lúc này, ta đã tính được quãng đường vật đi tiếp cho tới lúc dừng lại.

Định luật ll Niu tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{3-0,2\cdot0,5\cdot10}{0,5}=4\)m/s2
Vận tốc vât: \(v=a\cdot t=4\cdot2=8\)m/s

Chọn đáp án D
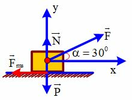
Lực tác dụng vào vật
+ Lực kéo động cơ F
+ Lực ma sát Fms
+ Trọng lực P
+ Phản lực của mặt sàn N
Theo định luật II Newton: ![]() (1)
(1)
Chọn hệ trục tọa độ xOy như hình vẽ
Chiếu (1) lên trục Oy: F sin 30 0 + N − P = 0 (2)
Chiếu (1) lên trục Ox: F cos 30 0 − Fms = ma (3)
Từ (2) → N = mg = −F sin 30 0
→ Fms= µN = P (mg − Fsin 30 0 ) (4)
Thế (4) vào (3), ta được: F cos 30 0 − µ(mg − Fsin 30 0 ) = ma (5)
Khi vật chuyển động với gia tốc a
+ Từ (5):

+ Với
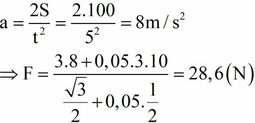

Áp dụng ĐL II Newton có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\) (*)
a. Để vật chuyển động thẳng đều thì \(a=0\)
Chiếu (*) lên phương thẳng đứng có:
\(N=P=mg=60\) (N)
Chiếu (*) lên phương chuyển động có:
\(F\cos45^o=F_{ms}\)
\(\Rightarrow F=\dfrac{0,1.60}{\cos45^o}=8,5\) (N)
b. Gia tốc của vật là:
\(a=\dfrac{2s}{t^2}=\dfrac{2.8}{4^2}=1\) (m/s2)
Khi đó:
\(F\cos45^o-F_{ms}=ma\)
\(\Rightarrow F=\dfrac{6.1+0,1.60}{cos45^o}=16,97\) (N)
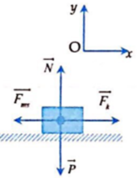
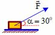
Chọn D.
Theo định luật II Niu - tơn:
P → + N → + F k → + F m s → = m a →
Chiếu lên trục Oy:
N – P = 0 => N = P = m.g = 15.10 = 150 (N)
⇒ F m s = μ . N = 0,05.150 = 7,5 ( N )
Chiếu lên trục Ox:
F k − F m s = m . a ⇒ a = F k − F m s m = 45 − 7,5 15 = 2,5 ( m / s 2 )
Quãng đường vật đi được sau 5s là
S = 1 2 a . t 2 = 1 2 .2,5.5 = 2 31,25 m