Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
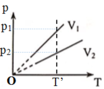
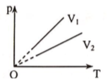
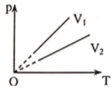
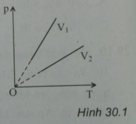
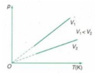
Vẽ đường đẳng nhiệt ứng với nhiệt độ T’ bất kỳ (vuông góc với trục OT), đường đẳng nhiệt này cắt các đường đẳng tích tại các điểm 1 và 2, từ 1 và 2 xác định p1 và p2; với quá trình đẳng nhiệt (ứng với nhiệt độ T’) ta có:
p1V1 = p2V2; vì p2 < p1 → V2 > V1

Chọn B.
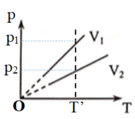
Vẽ đường đẳng nhiệt ứng với nhiệt độ T’ bất kỳ (vuông góc với trục OT), đường đẳng nhiệt này cắt các đường đẳng tích tại các điểm 1 và 2, từ 1 và 2 xác định p1 và p2; với quá trình đẳng nhiệt (ứng với nhiệt độ T’) ta có:
p 1 V 1 = p 2 V 2 ; vì p 2 < p 1 → V 2 > V 1

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)

Chọn B.
Từ (1) (2) thể tích không đổi, ta có:
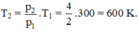
Từ (2) (3) áp suất không đổi, ta có:
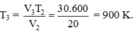
Suy ra: t3 = 627 oC.
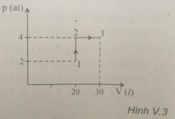
Đáp án B.
Vẽ đường đẳng nhiệt ứng với nhiệt độ T’ bất kỳ (vuông góc với trục OT), đường đẳng nhiệt này cắt các đường đẳng tích tại các điểm 1 và 2, từ 1 và 2 xác định p1 và P 2 ; với quá trình đẳng nhiệt (ứng với nhiệt độ T’) ta có:
p 1 V 1 = p 2 V 2 ; v ì p 2 < p 1 → V 2 > V 1