Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\dfrac{-1}{3}=\dfrac{-60}{120};\dfrac{-1}{4}=\dfrac{-30}{120}\)
=> ba số hữu tỉ xem giữa số \(\dfrac{-60}{120}\) và \(\dfrac{-30}{120}\)
=> Ba số hữu tỉ là: \(\dfrac{-40}{120};\dfrac{-45}{120};\dfrac{-55}{120}\)
Chúc bạn học tốt!!!
Ta có :
\(-\dfrac{1}{3}=-\dfrac{16}{48}\)
\(-\dfrac{1}{4}=-\dfrac{12}{48}\)
\(-\dfrac{16}{48}< -\dfrac{15}{48}< -\dfrac{14}{48}< -\dfrac{13}{48}< -\dfrac{12}{48}\)
Vậy 3 số hữu tỉ xen giữa \(-\dfrac{1}{3}\) và \(-\dfrac{1}{4}\) là : \(-\dfrac{15}{48};-\dfrac{14}{48};-\dfrac{13}{48}\)

\(\dfrac{-1}{2}=\dfrac{-1.12}{2.12}=\dfrac{-12}{24}\)
\(\dfrac{-1}{3}=\dfrac{-1.8}{3.8}=\dfrac{-8}{24}\)
Gọi các tỷ số đó là a
\(\dfrac{-12}{24}< a< \dfrac{-8}{24}\)
\(a\in\left\{\dfrac{-9}{24};\dfrac{-10}{24};\dfrac{-11}{24}\right\}\)
\(\dfrac{-1}{2}=-0,5\)
\(\dfrac{-1}{3}=-0,\left(3\right)\)
Suy ra \(-0,5< ...;...;...;< -0,\left(3\right)\)
\(\Rightarrow-0,5< -0,45< -0,44< -0,43< -0,\left(3\right)\)
\(\Rightarrow\dfrac{-1}{2}< \dfrac{-9}{20}< \dfrac{-11}{25}< \dfrac{-43}{100}< \dfrac{-1}{3}\)

a) Ta có : \(\frac{3}{4}=\frac{30}{40};\frac{3}{5}=\frac{24}{40}\)
\(\Rightarrow\)3 số hữu tỉ xen giữa 2 số \(\frac{30}{40}\)và \(\frac{24}{40}\)là : \(\frac{28}{40};\frac{26}{40};\frac{25}{40}\)
Vậy 3 số hữu tỉ xen giữa 2 số \(\frac{3}{4}\)và \(\frac{3}{5}\)là :\(\frac{7}{10};\frac{13}{20};\frac{5}{8}\)
Ta có : \(\frac{-1}{2}=\frac{-12}{24};\frac{-1}{3}=\frac{-8}{24}\)
\(\Rightarrow\)3 số hữu tỉ xen giữa 2 số \(\frac{-12}{24}\)và \(\frac{-8}{24}\)là : \(\frac{-9}{24};\frac{-10}{24};\frac{-11}{24}\)
Vậy 3 số hữu tỉ xen giữa 2 số : \(\frac{-1}{2}\)và \(\frac{-1}{3}\)là : \(\frac{-3}{8};\frac{-5}{12};\frac{-11}{24}\)
b) Ta có : \(\frac{2}{3}=\frac{8}{12};\frac{1}{6}=\frac{2}{12}\)
\(\Rightarrow\)5 số hữu tỉ xen giữa 2 số : \(\frac{8}{12}\)và \(\frac{2}{12}\)là : \(\frac{7}{12};\frac{6}{12};\frac{5}{12};\frac{4}{12};\frac{3}{12}\)
Vậy 5 số hữu tỉ xen giữa 2 số \(\frac{2}{3}\)và \(\frac{1}{6}\)là : \(\frac{7}{12};\frac{1}{2};\frac{5}{12};\frac{1}{3};\frac{1}{4}\)

Ba số hữu tỉ đó có dạng \(\dfrac{x}{y}\) với x; y ∈ Z, y ≠ 0
Theo bài ra: \(\dfrac{-1}{100}< \dfrac{x}{y}< \dfrac{1}{100}\)
⇒ \(\dfrac{-2}{200}< \dfrac{x}{y}< \dfrac{2}{200}\)
⇒ \(\dfrac{x}{y}\) ∈ \(\)\(\left\{-\dfrac{1}{200};0;\dfrac{1}{200};\right\}\)
Vậy ba số hữu tỉ cần tìm là: \(\dfrac{-1}{200};0;\dfrac{1}{200}\)

*\(\dfrac{1}{96}\)
*\(\dfrac{1}{26}\)
*\(\dfrac{1}{54}\)

Ta có : \(\dfrac{a}{b}\) < \(\dfrac{c}{d}\) => ad < bc (1)
Thêm ab và cả hai vế của (1) :
ad + ab < bc + ab
a(b+d) < b(a+c)
=> \(\dfrac{a}{b}\) < \(\dfrac{a+c}{b+d}\) (2)
Thêm cd vào hai vế của (1) :
ad + cd < bc + cd
d( a+c) < c( b+d )
=> \(\dfrac{a+c}{b+d}\) < \(\dfrac{c}{d}\) (3)
Từ (2) và (3) ta có : \(\dfrac{a}{b}\) < \(\dfrac{a+c}{b+d}\) < \(\dfrac{c}{d}\)

a, Theo đề bài ta có : \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\) \((1)\)
Thêm ab vào hai vế của 1 : \(ad+ab< bc+ab\)
\(a(b+d)< b(a+c)\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\) \((2)\)
Thêm cd vào hai vế của 1 : \(ad+cd< bc+cd\)
\(d(a+c)< c(b+d)\Rightarrow\frac{a+c}{b+d}< \frac{c}{d}\) \((3)\)
Từ 2 và 3 suy ra \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
b, Theo câu a ta lần lượt có :
\(\frac{-1}{3}< \frac{-1}{4}\Rightarrow\frac{-1}{3}< \frac{-2}{7}< \frac{-1}{4}\)
\(\frac{-1}{3}< \frac{-2}{7}\Rightarrow\frac{-1}{3}< \frac{3}{10}< \frac{-2}{7}\)
\(\frac{-1}{3}< \frac{-3}{10}\Rightarrow\frac{-1}{3}< \frac{-4}{13}< \frac{-3}{10}\)
Vậy : \(\frac{-1}{3}< \frac{-4}{13}< \frac{-3}{10}< \frac{-2}{7}< \frac{-1}{4}\)
a. ta có a\b < c\d nên
ad < bc
ad+ab < bc+ba
a( d+b) < b( c+a)
a\b < a+c\b+d (1)
ad<bc
ad +cd < bc+cd
d (a+c) < c(b+d)
a+c\b+d< c\d (2)
Từ 1 và 2 suy ra a\b < a+c\b+d < c\d
b. ta có -1\3 < -1\4
nên -1\3 < -2\7 < -3\11 < -4\15 < -1\4
c. Số hữu tỉ âm nhỏ hơn số tự nhiên là đúng

a) Ta có: \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
\(\Rightarrow ad+ab< bc+ab\)
\(\Rightarrow a\left(b+d\right)< b\left(a+c\right)\)
\(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\left(1\right)\)
Từ ad < bc
\(\Rightarrow ad+cd< bc+cd\)
\(\Rightarrow d\left(a+c\right)< c\left(b+d\right)\)
\(\Rightarrow\frac{c}{d}>\frac{a+c}{b+d}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
b) \(-\frac{1}{3}=-\frac{16}{48}< -\frac{15}{48}< -\frac{14}{48}< -\frac{13}{48}< -\frac{12}{48}=-\frac{1}{4}\)
Vậy 3 số hữu tỉ xen giữa \(-\frac{1}{3}và-\frac{1}{4}\)là \(-\frac{15}{48};-\frac{14}{48};-\frac{13}{48}\)
Ta có: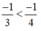
Áp dụng kết quả phần a) ta có:
Vậy ta có ba số hữu tỉ xen giữa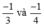 là:
là: