Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(tan^2a+cot^2a=\left(tana+cota\right)^2-2=m^2-2\)
\(tan^4a+cot^4a=\left(tan^2a+cot^2a\right)^2-2=\left(m^2-2\right)^2-2\)
\(tan^6a+cot^6a=\left(tan^2a+cot^2a\right)^3-3\left(tan^2a+cot^2a\right)\)
\(=\left(m^2-2\right)^3-3\left(m^2-2\right)\)
\(m^2=\left(tana+cota\right)^2=\left(tana-cota\right)^2+4tana.cota\)
\(\Rightarrow m^2=\left(tana-cota\right)^2+4\ge4\)
\(\Rightarrow\left|m\right|\ge2\)
a) \(tan^2\alpha+cot^2\alpha=\left(tan\alpha+cot\alpha\right)^2-2tan\alpha cot\alpha\)
\(=m^2-2\).
b) \(tan^3\alpha+cot^3\alpha=\left(tan\alpha+cot\alpha\right)\)\(\left(tan^2\alpha-tan\alpha cot\alpha+cot^2\alpha\right)\)
\(=m\left(tan^2\alpha+cot^2\alpha-tan\alpha cot\alpha\right)\)
\(=m\left(m^2-2-2\right)=m\left(m^2-3\right)\).
Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(tan\alpha< 0,cot\alpha< 0;cos\alpha< 0\).
Vì vậy: \(cos\alpha=-\sqrt{1-sin^2\alpha}=-\dfrac{\sqrt{7}}{4}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{3}{4}:\dfrac{-\sqrt{7}}{4}=\dfrac{-3}{\sqrt{7}}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{-\sqrt{7}}{3}\).
\(A=\dfrac{2tan\alpha-3cot\alpha}{cos\alpha+tan\alpha}\)\(=\dfrac{2.\dfrac{-3}{\sqrt{7}}-3.\dfrac{-\sqrt{7}}{3}}{\dfrac{-\sqrt{7}}{4}+\dfrac{-3}{\sqrt{7}}}\)
\(=\dfrac{\dfrac{-6}{\sqrt{7}}+\sqrt{7}}{\dfrac{-7-12}{4\sqrt{7}}}\)\(=\dfrac{\dfrac{-6+7}{\sqrt{7}}.4\sqrt{7}}{-19}\)\(=\dfrac{\dfrac{1}{\sqrt{7}}.4\sqrt{7}}{-19}=-\dfrac{4}{19}\).
b) \(\dfrac{cos^2\alpha+cot^2\alpha}{tan\alpha-cot\alpha}=\dfrac{\left(-\dfrac{\sqrt{7}}{4}\right)^2+\left(\dfrac{-\sqrt{7}}{3}\right)^2}{\dfrac{-3}{\sqrt{7}}+\dfrac{\sqrt{7}}{3}}\)
\(=\dfrac{\dfrac{7}{16}+\dfrac{7}{9}}{\dfrac{-9+7}{3\sqrt{7}}}=\dfrac{\dfrac{175}{144}}{\dfrac{-2}{3\sqrt{7}}}=\dfrac{-175}{96\sqrt{7}}\).
a) \(sin6\alpha cot3\alpha cos6\alpha=2.sin3\alpha.cos3\alpha\dfrac{cos3\alpha}{sin3\alpha}-cos6\alpha\)
\(=2cos^23\alpha-\left(2cos^23\alpha-1\right)=1\) (Không phụ thuộc vào x).
b) \(\left[tan\left(90^o-\alpha\right)-cot\left(90^o+\alpha\right)\right]^2\)\(-\left[cot\left(180^o+\alpha\right)+cot\left(270^o+\alpha\right)\right]^2\)
\(=\left[cot\alpha+cot\left(90^o-\alpha\right)\right]^2\)\(-\left[cot\alpha+cot\left(90^o+\alpha\right)\right]^2\)
\(=\left[cot\alpha+tan\alpha\right]^2-\left[cot\alpha-tan\alpha\right]^2\)
\(=4tan\alpha cot\alpha=4\). (Không phụ thuộc vào \(\alpha\)).
cotα = \(\frac{1}{3}\) \(\Leftrightarrow\frac{cos\alpha}{\sin\alpha}=\frac{1}{3}\Leftrightarrow\sin\alpha=3\cos\alpha\)
cotα =\(\frac{1}{\tan\alpha}=\frac{1}{3}\Rightarrow\tan\alpha=3\)
T = \(\frac{2016}{\sin^2\alpha-\sin\alpha\cos\alpha-\cos^2\alpha}=\frac{2016}{9\cos^2\alpha-3\cos^2\alpha-\cos^2\alpha}\) \(=\frac{2016}{5\cos^2\alpha}=\frac{2016}{5}\times\frac{1}{\cos^2\alpha}=\frac{2016}{5}\times\left(1+\tan^2\alpha\right)\) \(=\frac{2016}{5}\left(1+9\right)=4032\)
Ta có: \(\frac{\tan^2\alpha-\sin^2\alpha}{\cot^2\alpha-\cos^2\alpha}=\frac{\frac{\sin^2\alpha}{\cos^2\alpha}-\sin^2\alpha}{\frac{\cos^2\alpha}{\sin^2\alpha}-\cos^2\alpha}=\frac{\sin^2\alpha\left(\frac{1-\cos^2\alpha}{\cos^2\alpha}\right)}{\cos^2\alpha\left(\frac{1-\sin^2\alpha}{\sin^2\alpha}\right)}=\frac{\sin^2\alpha\left(\frac{\sin^2\alpha}{\cos^2\alpha}\right)}{\cos^2\alpha\left(\frac{\cos^2\alpha}{\sin^2\alpha}\right)}=\frac{\frac{\sin^4\alpha}{\cos^2\alpha}}{\frac{\cos^4\alpha}{\sin^2\alpha}}=\frac{\sin^4\alpha}{\cos^2\alpha}.\frac{\sin^2\alpha}{\cos^4\alpha}=\frac{\sin^6\alpha}{\cos^6\alpha}=\tan^6\alpha\)
P/s: Áp dụng công thức lượng giác cơ bản và liên hệ toán học giữa các hàm là đc :) Em lp 5 vậy nên sai thì thông cảm ạ
Chọn C.
Ta có :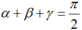
, suy ra
Suy ra :
⇒ cot α.cot γ =3.