PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
1
30 tháng 4 2020
\(\frac{15}{50}=\frac{15\cdot2}{50\cdot2}=\frac{30}{100}\)
\(\frac{7}{10}=\frac{7\cdot10}{10\cdot10}=\frac{70}{100}\)
\(\frac{24}{-20}=\frac{-24\cdot5}{20\cdot5}=\frac{-120}{100}\)
16 tháng 4 2016
bn xét hiệu giữa 2 số. nếu hiệu âm thì số bị trừ nhỏ hơn. còn nếu là số dương thì số bị trừ lớn hơn
16 tháng 4 2016
Ta có:
\(A=\frac{-7}{10^{2005}}+\frac{-15}{10^{2006}}=\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}+\frac{-8}{10^{2006}}=\left(\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}\right)+\frac{-8}{10^{2006}}\)
\(B=\frac{-15}{10^{2005}}+\frac{-7}{10^{2006}}=\frac{-7}{10^{2005}}+\frac{-8}{10^{2005}}+\frac{-7}{10^{2006}}=\left(\frac{-7}{10^{2005}}+\frac{-7}{10^{2006}}\right)+\frac{-8}{10^{2005}}\)
Vì \(-\frac{8}{10^{2006}}>-\frac{8}{10^{2005}}\)
\(\Rightarrow A>B\)
14 tháng 1 2024
a: \(\dfrac{-7}{15}=\dfrac{-7\cdot4}{15\cdot4}=\dfrac{-28}{60}\)
\(\dfrac{5}{12}=\dfrac{5\cdot5}{12\cdot5}=\dfrac{25}{60}\)
b: \(\dfrac{1}{5}=\dfrac{1\cdot6}{5\cdot6}=\dfrac{6}{30}\)
\(\dfrac{-2}{3}=\dfrac{-2\cdot10}{3\cdot10}=\dfrac{-20}{30}\)
\(\dfrac{7}{10}=\dfrac{7\cdot3}{10\cdot3}=\dfrac{21}{30}\)
c: \(\dfrac{-15}{50}=\dfrac{-15\cdot3}{50\cdot3}=\dfrac{-45}{150}\)
\(\dfrac{9}{10}=\dfrac{9\cdot15}{10\cdot15}=\dfrac{135}{150}\)
\(\dfrac{26}{-30}=\dfrac{-26}{30}=\dfrac{-26\cdot5}{30\cdot5}=\dfrac{-130}{150}\)
d: \(\dfrac{7}{10}=\dfrac{7\cdot51}{10\cdot51}=\dfrac{357}{510}\)
\(\dfrac{-5}{-15}=\dfrac{1}{3}=\dfrac{1\cdot170}{3\cdot170}=\dfrac{170}{510}\)
\(\dfrac{3}{17}=\dfrac{3\cdot30}{17\cdot30}=\dfrac{90}{510}\)
e: \(\dfrac{-4}{-75}=\dfrac{4}{75}=\dfrac{4}{75}\)
\(\dfrac{-3}{5}=\dfrac{-3\cdot15}{5\cdot15}=\dfrac{-45}{75}\)
\(\dfrac{8}{25}=\dfrac{8\cdot3}{25\cdot3}=\dfrac{24}{75}\)
f: \(-\dfrac{4}{5}=\dfrac{-4\cdot7}{5\cdot7}=\dfrac{-28}{35}\)
\(\dfrac{6}{7}=\dfrac{6\cdot5}{7\cdot5}=\dfrac{30}{35}\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
a) Ta có: BCNN(16, 24) = 48
48 : 16 = 3; 48 : 24 = 2. Do đó:
\(\frac{3}{{16}} = \frac{{3.3}}{{16.3}} = \frac{9}{{48}}\)
\(\frac{5}{{24}} = \frac{{5.2}}{{24.2}} = \frac{{10}}{{48}}\).
b) Ta có: BCNN(20, 30, 15) = 60
60 : 20 = 3; 60 : 30 = 2; 60 : 15 = 4. Do đó:
\(\frac{3}{{20}} = \frac{{3.3}}{{20.3}} = \frac{9}{{60}}\)
\(\frac{{11}}{{30}} = \frac{{11.2}}{{30.2}} = \frac{{22}}{{60}}\)
\(\frac{7}{{15}} = \frac{{7.4}}{{15.4}} = \frac{{28}}{{60}}\).
Q
17 tháng 4 2017
a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
PT
1
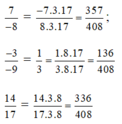
15 − 50 = − 3 10 ; 7 10 và 24 − 20 = - 12 10
sai quy đồng cơ mà