Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn mốc thế năng ở mặt đất.
a) Cơ năng ban đầu của vật: \(W_1=m.g.h_1=0,5.10.100=500(J)\)
Tại độ cao h2 = 50m thì thế năng là: \(W_{t2}=m.gh_2=0,5.10.50=250(J)\)
Cơ năng tại vị trí này: \(W_2=W_{đ2}+W_{t2}\)
Áp dụng định luật bảo toàn cơ năng ta có: \(W_2=W_1=500(J) \Rightarrow W_{đ2}=500-250=250(J)\)
b) Tại vị trí động năng bằng thế năng:
\(W_đ=W_t\Rightarrow W=2.W_t\Rightarrow m.g.h_1=2.m.g.h_3\)
\(\Rightarrow h_3=\dfrac{h_1}{2}=\dfrac{100}{2}=50(m)\)

a) Vị trí lực đàn hồi cân bằng với trọng lực:
kx0 = mg => x0 = 0,02 m = 2 cm.
b) Vận tốc của vật tại vị trí lực đàn hồi cân bằng với trọng lực:
1/2 . k(xo)2 = ½k(vcb)2 => |vcb| = 0,2√5 m/s = 20√5 (cm/s).
a. Ở vị trí cân bằng thì lực đàn hồi cân bằng với trọng lượng
\(\Rightarrow F_{đh}=P\Rightarrow k.\Delta l_0=mg\)
\(\Rightarrow \Delta l_0=\dfrac{mg}{k}=\dfrac{0,4.10}{200}=0,02m=2cm\)
b. Vị trí đó chính là vị trí cân bằng.
Chọn gốc thế năng ở vị trí cân bằng.
Thả vật ở vị trí lò xo không giãn \(\Rightarrow x_1=2cm\)
Áp dụng định luật bảo toàn cơ năng ta có:
\(\dfrac{1}{2}.k.x_1^2=\dfrac{1}{2}.m.v^2\)
\(\Rightarrow v = x_1.\sqrt{\dfrac{k}{m}}=2.\sqrt{\dfrac{200}{0,4}}==20\sqrt 5 (cm/s)\)

Chọn A.
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
Do có ma sát giữa vật và mặt phẳng nghiêng nên W2 – W1 = AFms
![]()

Chọn A.
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
Do có ma sát giữa vật và mặt phẳng nghiêng nên
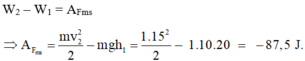

Chọn D.
Khi xảy ra va chạm đàn hồi xuyên tâm thì động lượng và động năng của hệ được bảo toàn. Do các vận tốc cùng phương nên
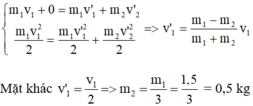

Chọn D.
Khi xảy ra va chạm đàn hồi xuyên tâm thì động lượng và động năng của hệ được bảo toàn. Do các vận tốc cùng phương nên
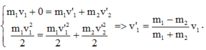
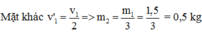

Chọn A