Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân có công bội
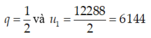
Khi đó diện tích mặt trên cùng là: .
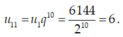

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

4.
Qua G kẻ đường thẳng song song AB lần lượt cắt AC và BC tại M và N
\(\Rightarrow A'B'NM\) là thiết diện của (A'B'G) và lăng trụ
Theo Talet ta có \(\frac{CM}{AC}=\frac{CN}{BC}=\frac{2}{3}\Rightarrow CM=CN=\frac{2a}{3}\)
Kéo dài A'M, B'N, C'C đồng quy tại P (theo tính chất giao tuyến 3 mặt phẳng)
Do \(CN//B'C'\Rightarrow\frac{PC}{PC'}=\frac{CN}{B'C'}=\frac{2}{3}\Rightarrow\frac{PC}{PC+CC'}=\frac{2}{3}\)
\(\Rightarrow3PC=2\left(PC+a\right)\Rightarrow PC=2a\)
\(\Rightarrow PC'=3a\)
\(MN=\frac{2}{3}BC\Rightarrow S_{CMN}=\frac{4}{9}S_{ABC}=\frac{4}{9}.\frac{a^2\sqrt{3}}{4}=\frac{a^2\sqrt{3}}{9}\)
\(V_{P.A'B'C'}=\frac{1}{3}PC'.S_{A'B'C'}=\frac{1}{3}.3a.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{4}\)
\(V_{P.CMN}=\frac{1}{3}PC.S_{CMN}=\frac{1}{3}.2a.\frac{a^2\sqrt{3}}{9}=\frac{2a^3\sqrt{3}}{27}\)
\(\Rightarrow V_{CMN.A'B'C'}=\frac{a^3\sqrt{3}}{4}-\frac{2a^3\sqrt{3}}{27}=\frac{19a^3\sqrt{3}}{108}\)
\(\Rightarrow V_{MNABA'B'}=\frac{a^3\sqrt{3}}{4}-\frac{19a^3\sqrt{3}}{108}=\frac{2a^3\sqrt{3}}{27}\)
2.
Đề thiếu dữ kiện ko tính được, chỉ tính được trong trường hợp tam giác ABC là vuông cân.
3.
\(AC=BC=a\sqrt{2}\) ; \(AC=AB\sqrt{2}=2a\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{BA'M}\) là góc giữa A'B và (ACC'A')
\(\Rightarrow\widehat{BA'M}=30^0\)
\(BM=\frac{1}{2}AC=a\)
\(tan\widehat{BA'M}=\frac{BM}{A'M}\Rightarrow A'M=\frac{BM}{tan30^0}=a\sqrt{3}\)
\(A'A=\sqrt{A'M^2-AM^2}=a\sqrt{2}\)
\(V=\frac{1}{2}A'A.AB.BC=a^3\sqrt{2}\)
Ko đáp án nào đúng




Chọn B.
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhan có công bội
Khi đó diện tích mặt trên cùng là: