
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Muốn chứng minh ba đường thẳng đồng quy ta chứng minh giao điểm của hai đường này là điểm chung của hai mặt phẳng mà giao tuyến là đường thứ ba

Muốn chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó là ba điểm chung của hai mặt phẳng phân biệt.

hứng minh đường thẳng song song với đường thẳng:
Để chứng minh hai đường thẳng song song, ta sử dụng các định lí.
- Ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng qui hoặc đôi một song song với nhau.
- Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
- Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa d và cắt (α) theo giao tuyến d’ thì d’ song song với d.
- Hai mặt phẳng phân biệt cùng song song với với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Một mặt phẳng cắt hai mặt phẳng song song cho hai giao tuyến song song.
- Sử dụng các phương pháp của hình học phẳng. Tính chất đường trung bình, định lí Ta-lét đảo, cạnh đối hình bình hành…
- Sử dụng tính chất về cạnh bên, cạnh đáy của hình lăng trụ.

Chứng minh đường thẳng song song với mặt phẳng
- Chứng minh d song song với đường thẳng d’ nằm trong (α) và d không thuộc(α).
- Có hai mặt phẳng song song, bất kì đường nào nằm trong hai mặt phẳng này cũng song song với mặt phẳng kia.

Gọi I = d1 ∩ d2; (P) là mặt phẳng chứa (d1) và (d2).
Gọi d3 ∩ d1 = M; d3 ∩ d2 = N.
+ M ∈ d1, mà d1 ⊂ (P) ⇒ M ∈ (P)
+ N ∈ d2, mà d2 ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ d3 có hai điểm M, N cùng thuộc (P)
⇒ d3 ⊂ (P)
⇒ d1; d2; d3 đồng phẳng (trái với giả thiết).
⇒ M ≡ N
⇒ M ≡ N ≡ I
Vậy d1; d2; d3 đồng quy.

Với n = 1 thì \(x^1\ge2.x^0=0\)
Giả sử đẳng thức đúng với n = k nghĩa là : \(x^k\ge\left(k+1\right).x^{k-1}\).
Ta phải chứng minh :
\(x^n\ge\left(n+1\right).x^{n-1}\)đúng với n = k + 1. Ta phải chứng minh \(x^{k+1}\ge\left[\left(k+1\right)+1\right].x^{\left(k-1\right)+1}=\left(k+2\right).x^k\)
\(=\left(x^k.k+2x^k+1\right)-1=\left(x^k+1\right)^2-1\le x^{k+1}\)
Vậy đẳng thức luôn đúng với mọi \(n\inℕ^∗\)
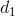 ,
, 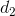 ,
,  là ba đường thẳng đã cho. Gọi I =
là ba đường thẳng đã cho. Gọi I =
Để chứng minh ba đường thẳng đồng quy, ta chứng minh:
– Ba đường thẳng ấy không đồng phẳng và đôi một cắt nhau.
– Ba đường thẳng ấy là các giao tuyến của ba mặt phẳng phân biệt đôi một cắt nhau và chúng không song song.