Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có: 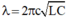
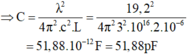
- Tụ xoay có điện dung tỉ lệ theo hàm bậc nhất với góc quay các bản tụ nên:
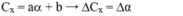
- Suy ra ta có tỉ lệ:
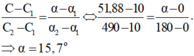

L của bạn đơn vị là \(2u H \) hay \(2\mu H \)
Mình sẽ làm với \(L = 2\mu H \)
Để bắt được sóng 19,2 m thì tụ C có giá trị là:
\(C = \frac{\lambda^2}{c^2.4.\pi^2.L} = \frac{19,2^2}{9.10^{16}.4.\pi^2.2.10^{-6}} = 51,9pF.\)
Như vậy cần phải xoay đến giá trị \(C = 51,9 pF.\)
\(0^0 \rightarrow 180^0: 10 pF \rightarrow 490pF. \)
\(0^0 \rightarrow \alpha ^0: 10 pF \rightarrow 51,9pF. \)
Khi đó ta có phương trình: \((180-0).(51,9-10) = (\alpha - 0).(490-10)\)
=> \(\alpha = \frac{180.41,9}{480} =15,7^0. \)
Chọn đáp án.C.15,70.

Đáp án B.
Điện dung của tụ phụ thuộc góc quay của bản tụ C = a. α + b
Với hai giá trị lớn nhất và nhỏ nhất của điện dung là C1 và C2 ta có
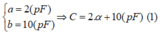
Để bắt được sóng có bước sóng λ = 22 , 3 m thì điện dung của tụ bằng
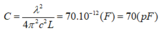
Thay vào (1) ta tìm được α = 30 0
Vậy phải tụ một góc bằng 1500 từ vị trí có điện dung cực đại (ứng với góc 1800).

Chọn D
Tụ xoay có điện dung biến thiên liên tục và tỉ lệ thuận với góc quay theo hàm bậc nhất nên ta có C = a.α + b (pF)
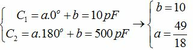
Khi α = 90 o → C = 255 p F
Bước sóng thu được:
![]()
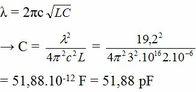




Chọn C
Tụ xoay có điện dung tỉ lệ theo hàm bậc nhất với góc quay các bản tụ nên điện dung của tụ điện: