Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng PT trạng thái khí lí tưởng: \(\dfrac{pV}{T}=const\)
+ Trong hệ tọa độ (V, T): Thể tích tỉ lệ với nhiệt độ
T V p1 p2
+ Trong hệ tọa độ (p, V)
v p p1 p2
+ Trong hệ tọa độ (p, T)
p p1 p2 T

Tính áp suất p' của khí trong bình .
Lúc đầu khí trong bình (1) có \(\begin{cases}V_1\\p=10^5Pa\\T=300K\end{cases}\) bình (2) có: \(\begin{cases}V_2=2V_1\\p\\T\end{cases}\)
Số mol khí trong hai bình \(n=\frac{3pV_1}{RT}\)
Lúc sau, khí trong bình (1) có \(\begin{cases}V_1\\p'\\T_1=273K\end{cases}\) bình (2) có \(\begin{cases}V_2=2V_1\\p'\\T_2=330K\end{cases}\)
Số mol khí trong bình (1): \(n_1=\frac{p'V_1}{RT_1}\), trong bình (2): \(n_2=\frac{2p'V_1}{RT_2}\)
\(n=n_1+n_2\Leftrightarrow\frac{3pV_1}{RT}=\frac{p'V_1}{RT_1}+\frac{2p'V_2}{RT_2}\)
\(\frac{3p}{T}=p'\left(\frac{1}{T_1}+\frac{2}{T_2}\right)\) suy ra \(p'=1,024.10^5Pa\)

Xét một khối lượng m của chất khí đó. Theo phương trình Menđêlêep - Clapêrông ta suy ra:
\(D=\frac{m}{V}=\frac{p}{RT}\mu\). Do đó ở trạng thái 1 và trạng thái 2 ta có:
\(D_1=\frac{m}{V_1}=\frac{p_1}{RT_1}\mu;\)\(D_2=\frac{m}{V_2}=\frac{p_2}{RT_2}\mu\).Từ đó: \(\frac{D_1}{D_2}=\frac{p_2T_2}{p_1T_1}\)
Suy ra biểu thức \(D_2=\frac{p_2T_2}{p_1T_1}D_1\)

a) Phần xi lanh bi nung nóng: \(\frac{P_oV_o}{T_o}=\frac{P_1V_1}{T_1}=\frac{P_1V_1}{T_0+\Delta T}\)
Phần xi lanh bị làm lạnh: \(\frac{P_oV_o}{T_o}=\frac{P_2V_2}{T_2}=\frac{P_2V_2}{T_0-\Delta T}\)
Vì P1 = P2 \(\rightarrow\frac{V_1}{V_2}=\frac{T_0+\Delta T}{T_0-\Delta T}\) (1)
Gọi đoạn di chuyển của pit-tông là x, ta có: V1 = (l + x)S và V2 = (l - x)S (2)
Từ (1) và (2) ta có \(\frac{\left(l+x\right)S}{\left(l-x\right)S}=\frac{T_0+\Delta T}{T_0-\Delta T}\rightarrow\) x = \(\frac{l\Delta T}{T_0}\)
b) P2V2 = P0V \(\rightarrow\) P2 = P0V0 /(l - x)S (1)
P1V1 = P0V \(\rightarrow\) P2 = P0V0/(l + x)S (2)
Xét pit-tông: F2 - F1 = ma \(\rightarrow\) (P2 - P1)S = ma (3)
Từ (1), (2), và (3)
\(\left(\frac{P_0V}{S\left(l-r\right)}\right)-\left(\frac{P_0V}{S\left(l+r\right)}\right)S\)= ma \(\rightarrow\) a = 2P0V0x/(l2 – x2)m
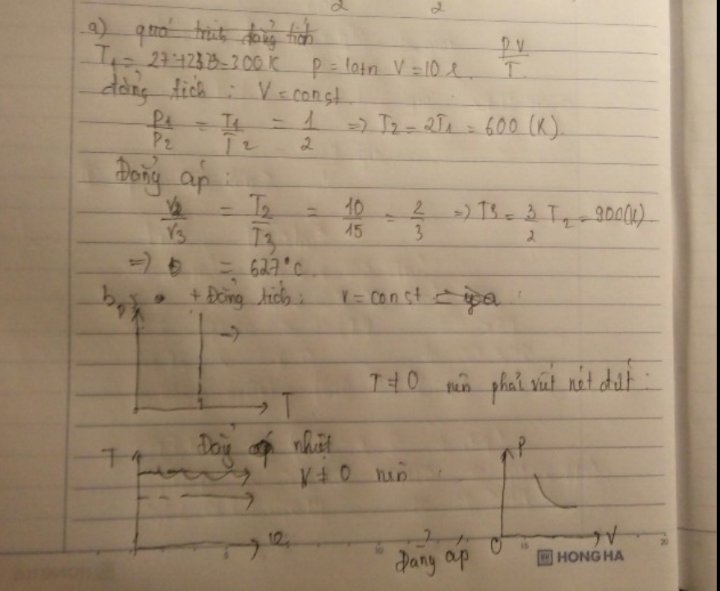
Đồ thị được biểu diễn trên hình 122
Nhận xét: Diện tích hình A V 1 V 2 B (phần gạch chéo) lớn hơn diện tích hình B V 2 V 3 C (phần nét chấm) nên công trong quá trình đẳng nhiệt ( A → B ) lớn hơn công trong quá trình đẳng áp ( B → C ).