Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án C
Giả sử phương trình dao động của vật có dạng : x = A cos ( ω t + φ )
ω = a m a x v m a x = 10 π rad / s
Biên độ : A = v m a x ω = 3 10 π m
Vận tốc của vật : v = x' = - ω A si n ( 10 πt + φ ) = - 3 sin ( 10 πt + φ ) m / s
v 0 = - 3 sin φ = 1,5 m/s ⇒ sin φ = - 0 , 5 s và do thế năng đang tăng nên chọn φ = - π 6

Phương trình có hai họ nghiệm 10 πt - π 6 = ± 2 π 3 ± 2 kπ
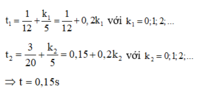

Đáp án C
+ t = 0 : v = + v m ax 2 ⇒ x = A 3 2 . Lúc này thế năng đang tăng suy ra x = A 3 2 và vật đi theo chiều dương.
+ thời điểm t : a = a m ax 2 ⇒ x = − A 2
Vòng tròn đơn vị :
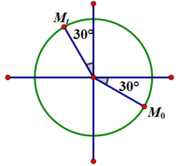
Vị trí của vật ở thời điểm t = 0 (M0) và t (Mt) như trên hình vẽ. Dễ dàng tìm được góc quét bằng 150 ° , tương ứng với Δ t = 5 T 12 .
Có
ω
=
a
m
ax
v
m
ax
=
10
π
⇒
T
=
0
,
2
(
s
)
⇒
Δ
t
=
0
,
083
(
s
)

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B
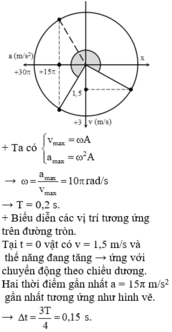
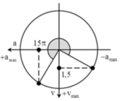

Đáp án D
Phương pháp: Sử dung̣ đường tròn lương̣ giác
Cách giải:
Theo bài ra ta có:
Thời điểm ban đầu vật ở vị trí (1) có v = v0/2
Khi
vật ở vị trí (2)
Từ hình vẽ xác định được thời điểm vật ở vị trí (2) là 5T/12 = 0,083s