Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(m_1=300g=0,3kg\)
\(t^0_1=100^0C\)
\(c_1=130\left(J/kg.K\right)\)
\(t^0_2=25^0C\)
\(c_2=4200\left(J/kg.K\right)\)
\(t^0_c=48^0C\)
________________________
\(m_2=?\)
Giải:
Nhiệt lượng của chì tỏa ra là:
\(Q_1=m_1\Delta t^0_1c_1=m_1\left(t^0_1-t^0_c\right)c_1=0,3.\left(100-48\right)130=2028\left(J\right)\)
Nhiệt lượng của nước thu vào là:
\(Q_2=m_2\Delta t^0_2c_2=m_2\left(t^0_c-t^0_2\right)c_2=m_2\left(48-25\right)4200=96600m_2\left(J\right)\)
Theo phương trình cân bằng nhiệt, ta có:
\(Q_1=Q_2\)
\(\Leftrightarrow2028=96600m_2\)
\(\Leftrightarrow m_2=\dfrac{2028}{96600}\approx0,021\left(g\right)\)
Vậy ...

1. Nhiệt độ của chì nay sau khi có sự cân bằng nhiệt là 40 độ C.
2. Nhiệt lượng nước thu vào là \(Q=C_{nước}.m_{nước}.\Delta t=4200.0,4.\left(40-30\right)=16800J.\)
3. Nhiệt lượng chì tỏa ra bằng nhiệt lượng nước thu vào tức là
\(Q_{tỏa}=Q_{thu}\)
=> \(C_{chì}.m_{chì}.\Delta t_2=16800\)
=> \(C_{chì}=\frac{16800}{1,25.80}=168\frac{J}{Kg.K}\)
1) nhiệt độ chì cân bằng là 40
2) nhiệt lượng nước là 16800
3) nhiệt dung riêng chì 168

Tóm tắt:
m1= 0,2kg
m2= ?
t1= 100°C
t2= 30°C
t= 35°C
-----------------------
a, Nhiệt lượng do miếng nhôm tỏa ra là:
Q1= m1*Cnhôm*(t1-t)= 0,2*880*(100-35)= 11440(J)
b, Nhiệt lương mà nước thu vào là:
Q2= m2*Cnước*(t-t2)= m2*4200*(35-30) (J)
Áp dụng phương trình cân bằng nhiệt:
Q1= Q2
<=> 11440= m2*4200*(35-30)
=> m2= 0,54 kg
Vậy nhiệt lượng do miếng nhôm tỏa ra là 11440J và khối lượng nước là 0,54kg

Tóm tắt
\(m_1=300g=0,3kg\\ t_1=100^0C\\ t_2=58,5^0C\\ t=60^0C\\ \Rightarrow\Delta t_1=t_1-t=100-60=40^0C\\ \Delta t_2=t-t_2=60-58,5=1,5^0C\\ c_1=130J/kg.K\\ c_2=4200J/kg.K\)
____________________
\(m_2=?kg\)
Giải
Theo phương trình cân bằng nhiệt ta có:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\Delta t_1=m_2.c_2.\Delta t_2\\ \Leftrightarrow0,3.130.40=m_2.4200.1,5\\ \Leftrightarrow m_2=0,25kg\)

Cho biết:
\(m_1=0,2kg\)
\(t_1=100^oC\)
\(t_1'=25^oC\)
\(t_2=30^oC\)
\(C_1=380J\)/kg.K
\(C_2=4200J\)/kg.K
Tìm:a) \(t_2=?\)
b) \(Q_1=?\)
c) \(m_2=?\)
Giải:
a) Sau khi thả quả cầu bằng đồng ở \(100^oC\)vào nước ở \(25^oC\) thì nhiệt độ cuối cùng của hệ là \(30^oC\) và đó cũng là nhiệt độ của quả cầu sau khi cân bằng.
b) Nhiệt lượng của quả cầu đồng tỏa ra:
\(Q_1=m_1C_1\left(t_1-t_2\right)\)
\(Q_1=0,2.380\left(100-30\right)\)
\(Q_1=5320\left(J\right)\)
c) Áp dụng phương trình cân bằng nhiệt, ta có:
\(Q_1=Q_2\)
Hay: \(5320=m_2C_2\left(t_2-t_1'\right)\)
\(5320=m_2.4200\left(30-25\right)\)
\(5320=21000m_2\)
\(m_2=0,253\left(kg\right)\)
Đáp số: a) \(t_2=30^oC\)
b) \(Q_1=5320J\)
c) \(m_2=0,253kg\)

Gọi khối lượng nước đá là M, khối lượng nước là m.
Ta có:\(\text{M+m = 25 kg (1)}\)
Và \(Q_{toa}=Q_{thu}\)
tức là: m.(60-25).c2c2 = M. (0 - (-50)). c1c1 + M. λ
\(\text{⇔ m.35.4200 = M.50.1800 + M.3,4. 10 ^5 }\)
\(\text{⇔ 147000m = 430000M (2)}\)
Từ (1) và (2) ta tìm được M ≈ 6,37 (kg) và m ≈18,63 kg

Ta có phương trình cân bằng nhiệt :
\(C_1.m_1.\left(t_1-t_{cb}\right)+C_2.m_2.\left(t_2-t_{cb}\right)=0\)
\(\Leftrightarrow880.m_1\left(150-50\right)+4200.0,75.\left(15-50\right)=0\)
\(\Leftrightarrow m_1=1,25\left(kg\right)\)
Vậy.....
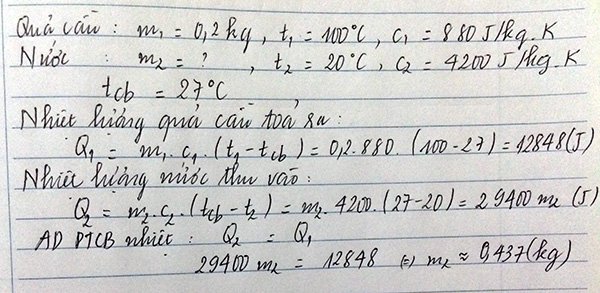
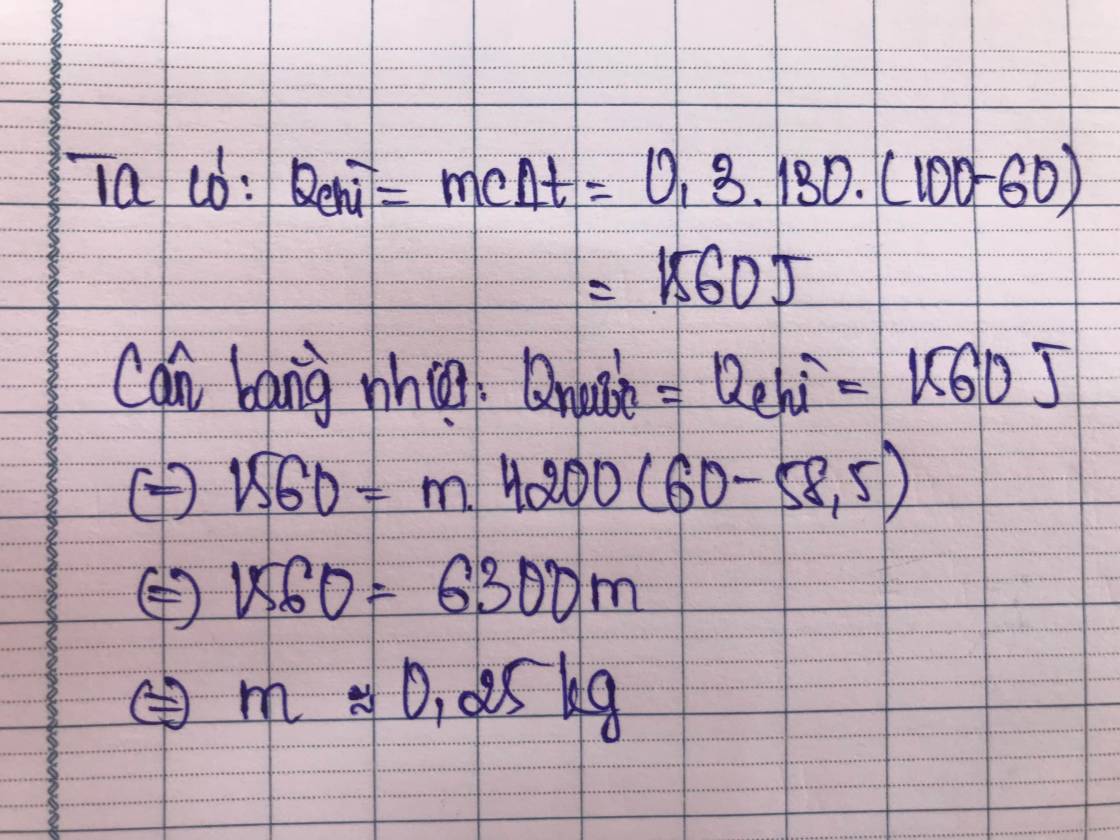

Nhiệt lượng tỏa ra của chì:
Q1=\(m_1.c_{chì}.\left(t_1-t_{cb}\right)\)
=0,3.130.(100-48)
=2028 J
Nhiệt lượng thu vào của nước
Q2=\(m_2.c_n.\left(t_{cb}-t_2\right)\)
=4200\(m_2\).(48-25)
=4200\(m_2.23\)
=96600\(m_2\)
Theo PT cân bằng nhiệt ta có:
Q1=Q2
2028=96600\(m_2\)
=> \(m_2\)=0,02kg=20g
Tóm tắt:
m1 = 300g = 0,3kg
t1o = 100oC
c1 = 130J/KgK
t2o = 25oC
c2 = 4200J/KgK
to = 48oC
-------------------------------------------
Nhiệt lượng của đồng tỏa ra là:
Qtỏa = \(m_1\cdot c_1\cdot\left(t_1^o-t^o\right)\)
= \(0,3\cdot130\cdot\left(100-48\right)\)
= \(2028\) (J)
Theo PTCBN, ta có:
Qtỏa = Qthu = 2028
Qthu = \(m_2\cdot c_2\cdot\left(t^o-t_2^o\right)\)
\(2028=m_2\cdot4200\cdot\left(48-25\right)\)
\(m_2=\dfrac{2028}{4200\cdot\left(48-25\right)}=0,02\) (kg)
Vậy khối lượng của nước trong cốc là 0,02kg
#ĐN