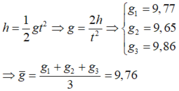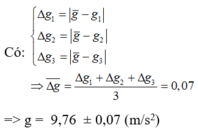Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn mốc thế năng tại mặt đất
a) Động năng lúc ném: \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.1.3^2=4,5(J)\)
Thế năng: \(W_t=mgh=1.10.1,5=15(J)\)
b) Ở vị trí cao nhất vận tốc bằng 0 nên động năng bằng 0
Cơ năng: \(W=W_đ+W_t=4,5+15=19,5(J)\)
c) Ở vị trí cao nhất, thế năng bằng cơ năng
\(\Rightarrow mg.h_{max}=19,5\Rightarrow h_{max}=1,95m\)

Đáp án B
Ban đầu ta cần phải treo con lắc đơn lên giá tại nơi cần xác định gia tốc trọng trường g. Sau đó dùng thước đo 5 lần chiều dài l của dây treo từ điểm treo tới tâm vật. Tiếp theo kích thích cho vật nhỏ dao động, rồi dùng đồng hồ bấm giây để đo thời gian của một dao động toàn phần để tính được chu kỳ T, lặp lại phép đo 5 lần. Dựa vào công thức trung bình tính giá trị trung bình của chiều dài và chu kỳ sau đó thay vào công thức để tính gia tốc trọng trường trung bình tại ví trí đó.

a)Chọn gốc thế năng tại mặt đất( điểm O)a) Gọi vị trí ném là A ,
\(W_A=\frac{1}{2}mv^0_2+mgh=\frac{1}{2}.0,1.10^2+0,1.10.10=15J\)
b)Gọi điểm cao nhất mà vật có thể đạt đk là : B
Cơ năng của vật tại B là : \(W_B=mg.OB\)
ADĐLBTCN : \(W_A=W_B\)
<=> mg.OB=15
<=> OB=15 (m)
c) Vận tốc khi chạm đất là :
\(V_đ=\sqrt{2g.OB}=\sqrt{2.10.15}\approx17,32\left(m\text{ /}s\right)\)
d) Gọi vị trí mà động năng =3/2 thế năng là D : \(W_đ=3\text{/}2W_t\)
-Cơ năng tại D là : \(W_D=W_t+W_đ=5\text{/}2W_t=5\text{/}2.mg.OD\)
ADĐLBTCN : \(W_A=W_D\)
<=> 5/2.mg.OD=15
<=> OD=6 (m)
Vậy : ....
Vậy độ cao cực đại mà vật đạt đk là 15m
a) Chọn gốc thế năng tại mặt đất (1)
Vị trí ném (2)
Ta có: \(W_2=\frac{1}{2}mv_2^2+mgz=\frac{1}{2}.0,1.10^2+0,1.10.10=15J\)
b) Độ cao cực đại vật đạt được (3)
Ta có: \(W_2=\frac{1}{2}mv_2^2\)
\(W_3=mgz_3\)
Áp dụng định luật bảo toàn cơ năng:
\(W_2=W_3\)
\(\Leftrightarrow\frac{1}{2}mv_2^2=mgz_3\)
\(\Rightarrow z_3=\frac{v_2^2}{2g}=5m\)
Độ cao cực đại mà vật đạt được so với mặt đất: 10+5=15m
c) Ta có: \(W_1=\frac{1}{2}mv_1^2\)
\(W_3=mgz_3\)
Áp dụng định luật bảo toàn cơ năng:
\(W_1=W_3\)
\(\Leftrightarrow\frac{1}{2}mv_1^2=mgz_3\)
\(\Rightarrow v_1=\sqrt{2gz_3}=10\sqrt{3}\)(m/s)
d) Vị trí mà \(W_đ=\frac{3}{2}W_t\) (4)
Ta có: \(W_4=W_{đ_4}+W_{t_4}\)
Áp dụng định luật bảo toàn cơ năng:
\(W_4=W_2\)
\(\Leftrightarrow W_{đ_4}+W_{t_4}=15\)
\(\Leftrightarrow\frac{3}{2}W_{t_4}+W_{t_4}=15\)
\(\Leftrightarrow\frac{5}{2}mgz_4=15\)
\(\Leftrightarrow z_4=6\left(m\right)\)

+ Vì cả 3 lần đo đều cho 1 kết quả nên L ¯ = 2 , 345 ¯ m
+ Sai số ngẫu nhiên DL = 0
+ Sai số của thiết bị là DL’ = 1 mm = 0,001 m
® L = (2,345 ± 0,001) m.
Đáp án C
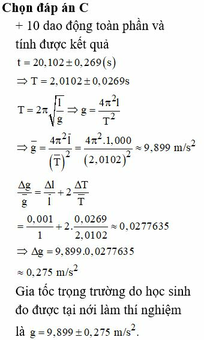

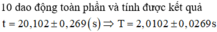
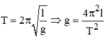

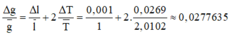

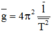
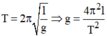
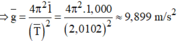
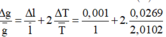

Đáp án B
Phương pháp: Công thức rơi tự do: h = g t 2 /2
Sử dụng công thức tính giá trị trung bình và công thức tính sai số
Cách giải:
Ta có: