Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để ý rằng đường chéo của hình lập phương chính là đường kính của khối cầu. Mặt khác ta lại có công thức: “Bình phương độ dài đường chéo của hình lập phương bằng ba lần bình phương của độ dài cạnh hình lập phương”. Khi đó 2 R 2 = 3 a 2 ⇒ a = 2 R 3 3
Suy ra V 1 = 2 3 3 R 3 = 8 3 9 R 3 .
Vì khối cầu có bán kính R nên ta có thể tính được bán kính và chiều cao của khối trụ ngoại tiếp ngoài khối cầu lần lượt là R và 2R.
Do đó V 2 = πR 2 . 2 = 2 πR 3
Vậy ta có tỉ số V 1 V 2 = 8 3 9 R 3 2 πR 3 = 4 3 9 π ≈ 0 , 245
Đáp án C

Đáp án B
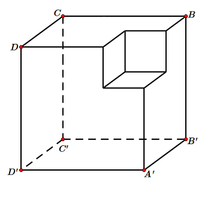
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC’ và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa mãn yêu cầu bài toán.
Ta có d I ; A ' B ' C ' D ' = d I ; B C C ' B ' = d I ; D C C ' D '
Suy ra I thuộc đoạn thẳng C’M và mặt cầu tâm I cần tìm đi qua điểm M.
Đặt d I ; D C C ' D ' = a , ta có IC' = a 3 mà A C ' = 3 3 , A M = 3
Suy ra I M = 2 3 - a 3 mặt khác d I ; D C C ' D ' = I M ⇔ a = 2 3 - a 3 ⇒ a = 3 - 3 3

Thiết diện qua trục hình nón là 1 tam giác đều cạnh x. Do đó bán kính đường tròn nội tiếp tam giác cũng chính là bán kính mặt cầu nội tiếp chóp là



Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .

Đáp án A
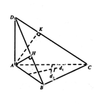
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Do tam giác AHB vuông tại H nên I thuộc trục của tam giác AHB. Tương tự I cũng thuộc trục của tam giác AKC. Suy ra I cách đều A, B, H,K, C nên nó là tâm mặt cầu ngoại tiếp hình chóp A.BCKH.
Gọi R là bán kính mặt cầu ngoại tiếp hình chóp A.BCKH thì R cũng là bán kính đường tròn ngoại tiếp tam giác ABC.
Ta có:
cot A + cot B + cot C = b 2 + c 2 - a 2 4 S + a 2 + c 2 - b 2 4 S + a 2 + b 2 - c 2 4 S = a 2 + b 2 + c 2 4 S
Nên c o t A + c o t B + c o t C 2 = B C A B . A C + C A B C . B A + A B C A . C B
⇔ a 2 + b 2 + c 2 8 S = a . sin A b c . sin A + b . sin B c a . sin B + c . sin C a b . sin C
⇔ a 2 + b 2 + c 2 8 S = a 2 4 R S + b 2 4 R S + c 2 4 R S ⇔ R = 2 ⇒ V = 4 3 πR 3 = 32 π 3

Đáp án B.
*Xác định tâm mặt cầu ngoại tiếp hình chóp A.BCHK
Gọi E, F lần lượt là trung điểm của AC và AB. Trong mặt phẳng (ABC), kẻ các đường thẳng d, d’ lần lượt vuông góc với AC và AB tại E, F. Do D A ⊥ d , D A ⊥ d ' (do D A ⊥ A B C ) nên d ⊥ D A C , d ' ⊥ D A B . Gọi I là giao điểm của d, d’ thì I chính là tâm của mặt cầu chứa hai đường tròn ngoại tiếp hai tam giác AHC, AKC. Hay nói cách khác, I là tâm mặt cầu ngoại tiếp hình chóp A.BCHK, bán kính R = IA cũng chính là bán kính đường tròn ngoại tiếp Δ A B C (do IA = IB = IC).
*Một số hệ thức cần nhớ trong tam giác
Cho Δ A B C , gọi AH là đường cao H ∈ B C . R, r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giac, p là nửa chu vi. Kí hiệu BC = a, AC = b, AB = c, diện tích S Δ A B C = S .
1. Định lý cosin:
a 2 = b 2 + c 2 − 2 b c cos A ; b 2 = a 2 + c 2 − 2 a c cos B ; c 2 = a 2 + b 2 − 2 a b cos C .
2. Định lý sin: a sin A = b sin B = c sin C = 2 R .
3. Độ dài trung tuyến xuất phát từ các đỉnh A, B, C (Kí hiệu lần lượt là m a , m b , m c ):
m a 2 = b 2 + c 2 2 − a 2 4 ; m b 2 = a 2 + c 2 2 − b 2 4 ; m c 2 = a 2 + b 2 2 − c 2 4 .4. Các công thức tính diện tích tam giác:
5. Định lý tang:
a − b a + b = tan A − B 2 tan A + B 2 ; b − c b + c = tan B − C 2 tan B + C 2 ; c − a c + a = tan C − A 2 tan C + A 2 .
6. Định lý cotang:
cot A = b 2 + c 2 − a 2 4 S ; cot B = a 2 + c 2 − b 2 4 S ; cot C = a 2 + b 2 − c 2 4 S . → cot A + cot B + cot C = a 2 + b 2 + c 2 4 S .
*Phân tích dữ kiện đề bài:
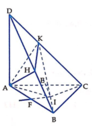
cot A + cot B + cot C 2 = B C A B . A C + C A B A . B C + A B C A . C B ⇔ A B 2 + B C 2 + C A 2 8 S Δ A B C = B C 2 + C A 2 + A B 2 A B . A C . B C ⇔ 8 S Δ A B C = A B . A C . B C ⇔ 8. A B . A C . B C 4 R = A B . A C . B C ⇔ R = 2 = I A .
Vậy thể tích mặt cầu ngoại tiếp hình chóp A.BCHK là:
V = 4 3 π R 3 = 4 3 π 2 3 = 32 π 3 (đvtt).

Đáp án C
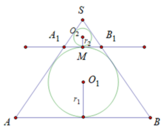
Ta dễ dàng nhìn thấy quy luật của thể tích các khối cầu
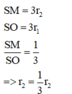
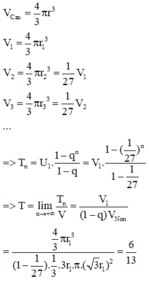



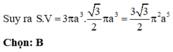
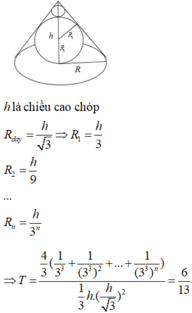
Đáp án D
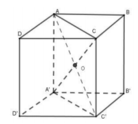
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là R 2 = A A ' 2 = a 2 ⇒ V 1 = 4 3 R 2 3 .
Bán kính mặt cầu ngoại tiếp khối cầu là
R 1 = A C ' 2 = A B 2 + A D 2 + A A ' 2 2 = a 3 2 ⇒ V 1 = 4 3 πR 3 1
Vậy tỉ số k = V 1 V 2 = R 3 1 R 3 1 = R 1 R 2 3 = 3 3 = 3 3 .