Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f=B.v./q/.sin(B,v)=1.28.10-15N
e chuyển động thẳng đều=>vecto(f)+vecto(F từ)
=>vecto(f) cùng phương ngược chiều f từ và f=F từ
F từ=1,28.10-5N=>E=\(\dfrac{F}{q}\)=......(trị q)=8000V/m
vecto E hướng xuống

Vì → q= e < 0 F → ↑ ↓ E →
Lực điện trường tác dụng lên electron: F → = q E → = m a →
→ a = q E m = − 1 , 6.10 − 19 .2.10 3 9 , 1.10 − 31 = − 0 , 35.10 15
Vì F → ↑ ↓ E → → a → ↑ ↓ v → 0
Tức là electron chuyển động chậm dần đều.
Quãng đường và thời gian vật đi được cho đến khi dừng lại là: v 2 − v 0 2 = 2 a s → 0 2 − 5.10 6 2 = 2 ( − 0 , 35.10 15 ) . s → s = 35 , 7.10 − 3 m = 3 , 57 c m
→ v = v 0 + a t → 0 = 5.10 6 − 0 , 35.10 15 → t = 14 , 3.10 − 9
Sau khi dừng lại, thì electron vẫn chịu tác dụng của lực điện trường như cũ nên nó sẽ chuyển động nhanh dần trở về vị trí xuất phát.
b. Gọi v → c là vận tốc của electron cuối đoạn đường l, ta có:
v c 2 − v 0 2 = 2 a l → v c 2 − 5.10 6 2 = 2 ( − 0 , 35.10 15 ) .10 − 2 → v c = 18.10 12
Trong trường hợp này thì khi electron đi hết đoạn đường l cũng là lúc nó ra khỏi điện trường nên không còn tác dụng của lực điện trường nữa. Do đó nó sẽ chuyển động thẳng đều.

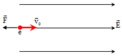
Để giải bài tập này thì em chú ý đến hiện tượng như sau: Ban đầu thì điện tích chuyển động với vận tốc v cùng hướng với đường sức và lúc này electron chịu tác dụng của lực điện ngược chiều điện trường => Đến vị trí A nào đó điện tích sẽ có vận tốc = 0. Và lực điện kéo điện tích lại vị trí ban đầu O.
O A v q<0 E F
Gai đoạn 1 (O-A): AD Định lí biến thiên động năng:
\(\frac{1}{2}mv^2_2-\frac{1}{2}mv^2=A_F=qEd\)
\(\Rightarrow0-\frac{1}{2}mv^2=-1,6.10^{-19}.182.d\Rightarrow d=0,16m\) với \(m_e=9,1.10^{-31}kg;v=3200000\)m/s.
\(v^2-v_1^2=2aS\Rightarrow a=0^2-\frac{\left(32.10^5\right)^2}{2S}=-3,8.10^{13}\) m/s^2
\(\Rightarrow v=v_0+at\Rightarrow t=8,42.10^8s\)
Giai đoạn 2(A-O): Tương tự \(t_2=t_1\)
Vậy thời gian để e trở lại vị trí ban đầu là \(t=1,68.10^7s\)
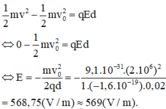
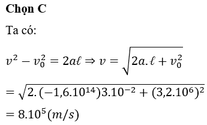

Chọn A
Áp dụng định lý động năng ta có: